| Tetraoctagonal tiling | |
|---|---|
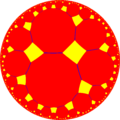
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (4.8)2 |
| Schläfli symbol | r{8,4} or rr{8,8} rr(4,4,4) t0,1,2,3(∞,4,∞,4) |
| Wythoff symbol | 2 | 8 4 |
| Coxeter diagram |     or   or        |
| Symmetry group | [8,4], (*842) [8,8], (*882) [(4,4,4)], (*444) [(∞,4,∞,4)], (*4242) |
| Dual | Order-8-4 quasiregular rhombic tiling |
| Properties | Vertex-transitive edge-transitive |
In geometry, the tetraoctagonal tiling is a uniform tiling of the hyperbolic plane.
There are for uniform constructions of this tiling, three of them as constructed by mirror removal from the [8,4] or (*842) orbifold symmetry. Removing the mirror between the order 2 and 4 points, [8,4,1+], gives [8,8], (*882). Removing the mirror between the order 2 and 8 points, [1+,8,4], gives [(4,4,4)], (*444). Removing both mirrors, [1+,8,4,1+], leaves a rectangular fundamental domain, [(∞,4,∞,4)], (*4242).
| Name | Tetra-octagonal tiling | Rhombi-octaoctagonal tiling | ||
|---|---|---|---|---|
| Image |  |  |  |  |
| Symmetry | [8,4] (*842)    | [8,8] = [8,4,1+] (*882)  =  | [(4,4,4)] = [1+,8,4] (*444) =  | [(∞,4,∞,4)] = [1+,8,4,1+] (*4242) = or  |
| Schläfli | r{8,4} | rr{8,8} =r{8,4}1/2 | r(4,4,4) =r{4,8}1/2 | t0,1,2,3(∞,4,∞,4) =r{8,4}1/4 |
| Coxeter | | = | = | = or |
The dual tiling has face configuration V4.8.4.8, and represents the fundamental domains of a quadrilateral kaleidoscope, orbifold (*4242), shown here. Adding a 2-fold gyration point at the center of each rhombi defines a (2*42) orbifold.
 |  |
| *n42 symmetry mutations of quasiregular tilings: (4.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *4n2 [n,4] | Spherical | Euclidean | Compact hyperbolic | Paracompact | Noncompact | |||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | [ni,4] | |
| Figures |  |  |  |  |  |  |  | |
| Config. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.ni)2 |
| Dimensional family of quasiregular polyhedra and tilings: (8.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *8n2 [n,8] | Hyperbolic... | Paracompact | Noncompact | ||||||||
| *832 [3,8] | *842 [4,8] | *852 [5,8] | *862 [6,8] | *872 [7,8] | *882 [8,8]... | *∞82 [∞,8] | [iπ/λ,8] | ||||
| Coxeter |  | |  |  |  | |  |  | |||
| Quasiregular figures configuration |  3.8.3.8 | 4.8.4.8 |  8.5.8.5 |  8.6.8.6 |  8.7.8.7 |  8.8.8.8 |  8.∞.8.∞ | 8.∞.8.∞ | |||
| Uniform octagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (And [(∞,4,∞,4)] (*4242) index 4 subsymmetry) | |||||||||||
=  =  = | = | = = = | = | =  = | = | | |||||
 |  |  |  |  |  |  | |||||
| {8,4} | t{8,4} | r{8,4} | 2t{8,4}=t{4,8} | 2r{8,4}={4,8} | rr{8,4} | tr{8,4} | |||||
| Uniform duals | |||||||||||
 | | | | | | | |||||
 |  |  |  |  |  |  | |||||
| V84 | V4.16.16 | V(4.8)2 | V8.8.8 | V48 | V4.4.4.8 | V4.8.16 | |||||
| Alternations | |||||||||||
| [1+,8,4] (*444) | [8+,4] (8*2) | [8,1+,4] (*4222) | [8,4+] (4*4) | [8,4,1+] (*882) | [(8,4,2+)] (2*42) | [8,4]+ (842) | |||||
 =  |  =  | =   | =  | =  | = | | |||||
 |  |  |  |  |  |  | |||||
| h{8,4} | s{8,4} | hr{8,4} | s{4,8} | h{4,8} | hrr{8,4} | sr{8,4} | |||||
| Alternation duals | |||||||||||
 | | | | | | | |||||
 |  |  |  |  | |||||||
| V(4.4)4 | V3.(3.8)2 | V(4.4.4)2 | V(3.4)3 | V88 | V4.44 | V3.3.4.3.8 | |||||
| Uniform octaoctagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [8,8], (*882) | |||||||||||
=   = | = = | = = | =  = | = = | = = | = = | |||||
 |  |  |  |  |  |  | |||||
| {8,8} | t{8,8} | r{8,8} | 2t{8,8}=t{8,8} | 2r{8,8}={8,8} | rr{8,8} | tr{8,8} | |||||
| Uniform duals | |||||||||||
| | | | | | | |||||
 |  |  |  |  |  |  | |||||
| V88 | V8.16.16 | V8.8.8.8 | V8.16.16 | V88 | V4.8.4.8 | V4.16.16 | |||||
| Alternations | |||||||||||
| [1+,8,8] (*884) | [8+,8] (8*4) | [8,1+,8] (*4242) | [8,8+] (8*4) | [8,8,1+] (*884) | [(8,8,2+)] (2*44) | [8,8]+ (882) | |||||
| = | | = | | =  | = = | = = | |||||
 | | | |  | |||||||
| h{8,8} | s{8,8} | hr{8,8} | s{8,8} | h{8,8} | hrr{8,8} | sr{8,8} | |||||
| Alternation duals | |||||||||||
| | | | | | | |||||
 |  | ||||||||||
| V(4.8)8 | V3.4.3.8.3.8 | V(4.4)4 | V3.4.3.8.3.8 | V(4.8)8 | V46 | V3.3.8.3.8 | |||||
| Uniform (4,4,4) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,4)], (*444) | [(4,4,4)]+ (444) | [(1+,4,4,4)] (*4242) | [(4+,4,4)] (4*22) | ||||||||
 | | | | | | | | | | ||
 |  |  |  |  |  |  |  | |  | ||
| t0(4,4,4) h{8,4} | t0,1(4,4,4) h2{8,4} | t1(4,4,4) {4,8}1/2 | t1,2(4,4,4) h2{8,4} | t2(4,4,4) h{8,4} | t0,2(4,4,4) r{4,8}1/2 | t0,1,2(4,4,4) t{4,8}1/2 | s(4,4,4) s{4,8}1/2 | h(4,4,4) h{4,8}1/2 | hr(4,4,4) hr{4,8}1/2 | ||
| Uniform duals | |||||||||||
 |  |  |  |  |  |  |  | |  | ||
| V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V88 | V(4,4)3 | ||
In geometry, the truncated tetrahexagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{6,4}.
In geometry, the tetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol r{6,4}.
In geometry, the rhombitetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{6,4}. It can be seen as constructed as a rectified tetrahexagonal tiling, r{6,4}, as well as an expanded order-4 hexagonal tiling or expanded order-6 square tiling.
In geometry, the truncated order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,4}. A secondary construction tr{6,6} is called a truncated hexahexagonal tiling with two colors of dodecagons.
In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.
In geometry, the truncated tetrapentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1,2{4,5} or tr{4,5}.
In geometry, the order-6 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,6} and is self-dual.
In geometry, the order-4 octagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {8,4}. Its checkerboard coloring can be called a octaoctagonal tiling, and Schläfli symbol of r{8,8}.
In geometry, the truncated order-4 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{8,4}. A secondary construction t0,1,2{8,8} is called a truncated octaoctagonal tiling with two colors of hexakaidecagons.
In geometry, the order-8 square tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {4,8}.
In geometry, the rhombitetraoctagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{8,4}. It can be seen as constructed as a rectified tetraoctagonal tiling, r{8,4}, as well as an expanded order-4 octagonal tiling or expanded order-8 square tiling.
In geometry, the truncated tetraoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,4}.
In geometry, the truncated order-8 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{8,8}.
In geometry, the order-4 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,4}.
In geometry, the truncated tetraapeirogonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one apeirogon on each vertex. It has Schläfli symbol of tr{∞,4}.
In geometry, the rhombitetraapeirogonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{∞,4}.
In geometry, the order-6 octagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {8,6}.
In geometry, the order-8 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,8}.
In geometry, the hexaoctagonal tiling is a uniform tiling of the hyperbolic plane.
In geometry, the truncated order-8 hexagonal tiling is a semiregular tiling of the hyperbolic plane. It has Schläfli symbol of t{6,8}.
