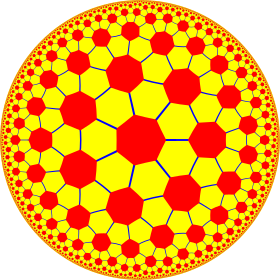
In geometry, a heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex. It has Schläfli symbol of r{7,3}.
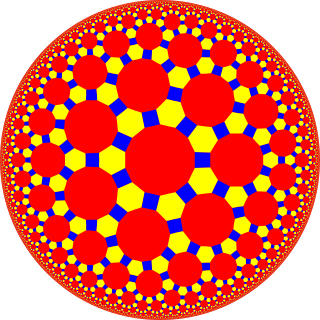
In geometry, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one square, one hexagon, and one tetradecagon (14-sides) on each vertex. It has Schläfli symbol of tr{7,3}.

In geometry, the truncated heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one triangle and two tetradecagons on each vertex. It has Schläfli symbol of t{7,3}. The tiling has a vertex configuration of 3.14.14.

In geometry, the rhombitriheptagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one heptagon, alternating between two squares. The tiling has Schläfli symbol rr{7, 3}. It can be seen as constructed as a rectified triheptagonal tiling, r{7,3}, as well as an expanded heptagonal tiling or expanded order-7 triangular tiling.
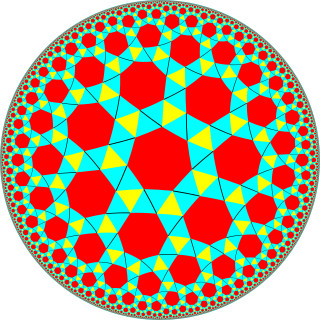
In geometry, the order-3 snub heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles and one heptagon on each vertex. It has Schläfli symbol of sr{7,3}. The snub tetraheptagonal tiling is another related hyperbolic tiling with Schläfli symbol sr{7,4}.

In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}.

In geometry, the rhombitetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{6,4}. It can be seen as constructed as a rectified tetrahexagonal tiling, r{6,4}, as well as an expanded order-4 hexagonal tiling or expanded order-6 square tiling.
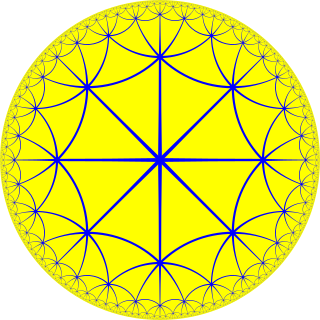
In geometry, the order-8 triangular tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {3,8}, having eight regular triangles around each vertex.
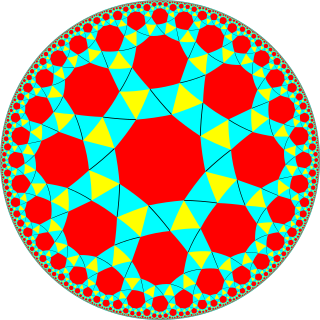
In geometry, the order-3 snub octagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles, one octagon on each vertex. It has Schläfli symbol of sr{8,3}.

In geometry, the truncated order-8 triangular tiling is a semiregular tiling of the hyperbolic plane. There are two hexagons and one octagon on each vertex. It has Schläfli symbol of t{3,8}.

In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.
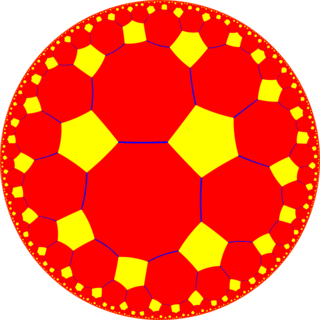
In geometry, the truncated order-5 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{5,5}, constructed from one pentagons and two decagons around every vertex.

In geometry, the order-4 heptagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {7,4}.

In geometry, the truncated order-4 heptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{7,4}.

In geometry, the order-7 heptagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {7,7}, constructed from seven heptagons around every vertex. As such, it is self-dual.

In geometry, the truncated order-7 heptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{7,7}, constructed from one heptagons and two tetrakaidecagons around every vertex.

In geometry, the snub heptaheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{7,7}, constructed from two regular heptagons and three equilateral triangles around every vertex.

In geometry, the order-5 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,5}.