
Dividing a square into similar rectangles (or, equivalently, tiling a square with similar rectangles) is a problem in mathematics.

Dividing a square into similar rectangles (or, equivalently, tiling a square with similar rectangles) is a problem in mathematics.
There is only one way (up to rotation and reflection) to divide a square into two similar rectangles.
However, there are three distinct ways of partitioning a square into three similar rectangles: [1] [2]
The fact that a rectangle of aspect ratio ρ2 can be used for dissections of a square into similar rectangles is equivalent to an algebraic property of the number ρ2 related to the Routh–Hurwitz theorem: all of its conjugates have positive real part. [3] [4]
In 2022, the mathematician John Baez brought the problem of generalizing this problem to n rectangles to the attention of the Mathstodon online mathematics community. [5] [6]
The problem has two parts: what aspect ratios are possible, and how many different solutions are there for a given n. [7] Frieling and Rinne had previously published a result in 1994 that states that the aspect ratio of rectangles in these dissections must be an algebraic number and that each of its conjugates must have a positive real part. [3] However, their proof was not a constructive proof.
Numerous participants have attacked the problem of finding individual dissections using exhaustive computer search of possible solutions. One approach is to exhaustively enumerate possible coarse-grained placements of rectangles, then convert these to candidate topologies of connected rectangles. Given the topology of a potential solution, the determination of the rectangle's aspect ratio can then trivially be expressed as a set of simultaneous equations, thus either determining the solution exactly, or eliminating it from possibility. [8]
As of March 2023 [update] , the following results (sequence A359146 in the OEIS ) have been obtained for the number of distinct valid dissections for different values of n: [7] [9] [10]
| n | # of dissections |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 11 |
| 5 | 51 |
| 6 | 245 |
| 7 | 1372 |
| 8 | 8522 |

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if

Derived from the Greek word for '5', and "domino", a pentomino is a polyomino of order 5; that is, a polygon in the plane made of 5 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.

Squaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.

In geometry, the Wallace–Bolyai–Gerwien theorem, named after William Wallace, Farkas Bolyai and P. Gerwien, is a theorem related to dissections of polygons. It answers the question when one polygon can be formed from another by cutting it into a finite number of pieces and recomposing these by translations and rotations. The Wallace–Bolyai–Gerwien theorem states that this can be done if and only if two polygons have the same area.

An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types is aperiodic if copies of these tiles can form only non-periodic tilings.

In information visualization and computing, treemapping is a method for displaying hierarchical data using nested figures, usually rectangles.

In mathematics, the plastic ratio is a geometrical proportion close to 53/40. Its true value is the real solution of the equation x3 = x + 1.
14 (fourteen) is a natural number following 13 and preceding 15.
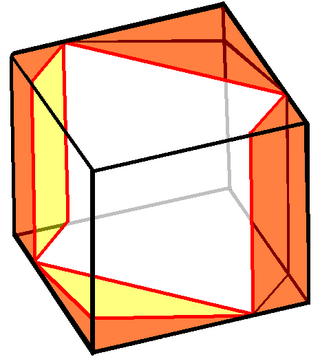
In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into separate pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square. Equivalently, the problem is to arrange n points in a unit square aiming to get the greatest minimal separation, dn, between points. To convert between these two formulations of the problem, the square side for unit circles will be L = 2 + 2/dn.

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.

In geometry, an equidissection is a partition of a polygon into triangles of equal area. The study of equidissections began in the late 1960s with Monsky's theorem, which states that a square cannot be equidissected into an odd number of triangles. In fact, most polygons cannot be equidissected at all.
David Anthony Klarner was an American mathematician, author, and educator. He is known for his work in combinatorial enumeration, polyominoes, and box-packing.
Edmund Orme Harriss is a British mathematician, writer and artist. Since 2010 he has been at the Fulbright College of Arts & Sciences at The University of Arkansas in Fayetteville, Arkansas where he is an Assistant Professor of Arts & Sciences (ARSC) and Mathematical Sciences (MASC). He does research in the Geometry of Tilings and Patterns, a branch of Convex and Discrete Geometry. He is the discoverer of the spiral that bears his name.