
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 168 × 2 = 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2, 7), the second-smallest non-abelian simple group after the alternating group A5. The quartic was first described in (Klein 1878b).
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action.

In geometry, the truncated trihexagonal tiling is one of eight semiregular tilings of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{3,6}.

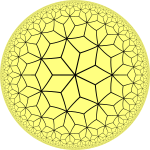
In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.

In geometry, a heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex. It has Schläfli symbol of r{7,3}.
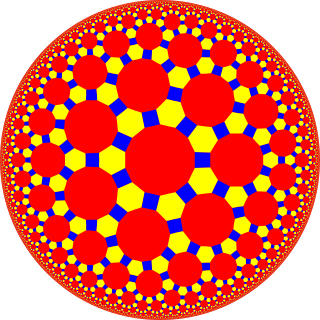
In geometry, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one square, one hexagon, and one tetradecagon (14-sides) on each vertex. It has Schläfli symbol of tr{7,3}.

In geometry, the truncated heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one triangle and two tetradecagons on each vertex. It has Schläfli symbol of t{7,3}. The tiling has a vertex configuration of 3.14.14.

In geometry, the rhombitriheptagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one heptagon, alternating between two squares. The tiling has Schläfli symbol rr{7, 3}. It can be seen as constructed as a rectified triheptagonal tiling, r{7,3}, as well as an expanded heptagonal tiling or expanded order-7 triangular tiling.
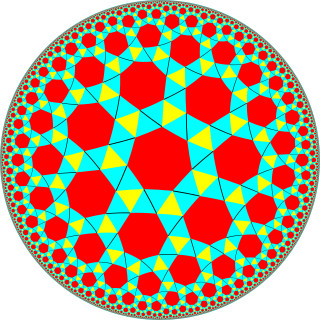
In geometry, the order-3 snub heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles and one heptagon on each vertex. It has Schläfli symbol of sr{7,3}. The snub tetraheptagonal tiling is another related hyperbolic tiling with Schläfli symbol sr{7,4}.

In geometry, the order-7 truncated triangular tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons. It has Schläfli symbol of t{3,7}.
In hyperbolic geometry, a uniform hyperbolic tiling is an edge-to-edge filling of the hyperbolic plane which has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent, and the tiling has a high degree of rotational and translational symmetry.

In geometry, the 4-5 kisrhombille or order-4 bisected pentagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 8, and 10 triangles meeting at each vertex.

In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}.
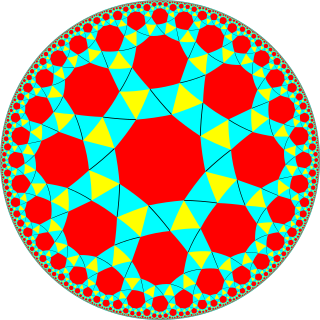
In geometry, the order-3 snub octagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles, one octagon on each vertex. It has Schläfli symbol of sr{8,3}.
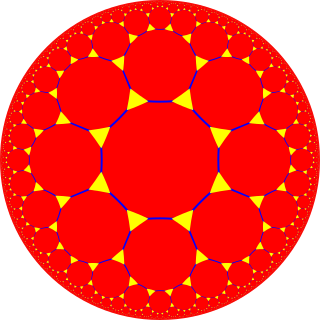
In geometry, the truncated octagonal tiling is a semiregular tiling of the hyperbolic plane. There is one triangle and two hexakaidecagons on each vertex. It has Schläfli symbol of t{8,3}.

In geometry, the order-3 apeirogonal tiling is a regular tiling of the hyperbolic plane. It is represented by the Schläfli symbol {∞,3}, having three regular apeirogons around each vertex. Each apeirogon is inscribed in a horocycle.
In the geometry of hyperbolic 3-space, the order-7-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,7,3}.
















































![Visualization of the map (2,3,[?]) - (2,3,7) by morphing the associated tilings. Morphing of modular tiling to 2 3 7 triangle tiling.gif](http://upload.wikimedia.org/wikipedia/commons/thumb/1/15/Morphing_of_modular_tiling_to_2_3_7_triangle_tiling.gif/220px-Morphing_of_modular_tiling_to_2_3_7_triangle_tiling.gif)

















