| Hexagonal bipyramid | |
|---|---|
 | |
| Type | bipyramid |
| Faces | 12 triangles |
| Vertices | 8 |
| Vertex configuration | V4.4.6 |
| Schläfli symbol | { } + {6} |
| Coxeter diagram | |
| Symmetry group | D6h, [6,2], (*226), order 24 |
| Rotation group | D6, [6,2]+, (226), order 12 |
| Dual polyhedron | hexagonal prism |
| Properties | convex, face-transitive |
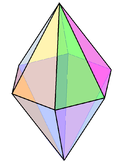
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.
Contents
Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have six faces, and it is not a Johnson solid because its faces cannot be equilateral triangles; 6 equilateral triangles would make a flat vertex.
It is one of an infinite set of bipyramids. Having twelve faces, it is a type of dodecahedron, although that name is usually associated with the regular polyhedral form with pentagonal faces.
The hexagonal bipyramid has a plane of symmetry (which is horizontal in the figure to the right) where the bases of the two pyramids are joined. This plane is a regular hexagon. There are also six planes of symmetry crossing through the two apices. These planes are rhombic and lie at 30° angles to each other, perpendicular to the horizontal plane.