In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids, and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.
In geometry, an octahedron is a polyhedron with eight faces. An octahedron can be considered as a square bipyramid. When the edges of a square bipyramid are all equal in length, it produces a regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. It is also an example of a deltahedron. An octahedron is the three-dimensional case of the more general concept of a cross polytope.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.
In geometry, the term semiregular polyhedron is used variously by different authors.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, a trigonal trapezohedron is a polyhedron with six congruent quadrilateral faces, which may be scalene or rhomboid. The variety with rhombus-shaped faces faces is a rhombohedron. An alternative name for the same shape is the trigonal deltohedron.
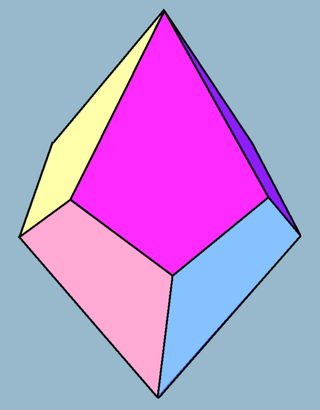
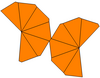
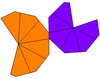
In geometry, a tetragonal trapezohedron, or deltohedron, is the second in an infinite series of trapezohedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism.

In geometry, a pentagonal trapezohedron is the third in an infinite series of face-transitive polyhedra which are dual polyhedra to the antiprisms. It has ten faces which are congruent kites.

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

In geometry, a tessellation of dimension 2 or higher, or a polytope of dimension 3 or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be transitive, i.e. must lie within the same symmetry orbit. In other words, for any two faces A and B, there must be a symmetry of the entire figure by translations, rotations, and/or reflections that maps A onto B. For this reason, convex isohedral polyhedra are the shapes that will make fair dice.
In geometry, a polytope or a tiling is isotoxal or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other while leaving the region occupied by the object unchanged.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion: it moves the faces apart (outward), and adds a new face between each two adjacent faces; but contrary to expansion, it maintains the original vertices. For a polyhedron, this operation adds a new hexagonal face in place of each original edge.