
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as a rectangular cuboid with six square faces, or a parallelepiped with equal edges. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, an octahedron is a polyhedron with eight faces. An octahedron can be considered as a square bipyramid. When the edges of a square bipyramid are all equal in length, it produces a regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. It is also an example of a deltahedron. An octahedron is the three-dimensional case of the more general concept of a cross polytope.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
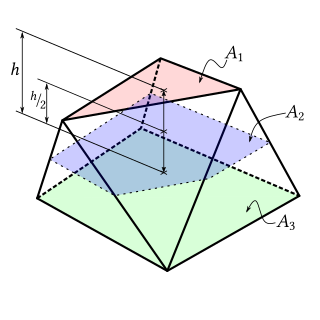
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid.
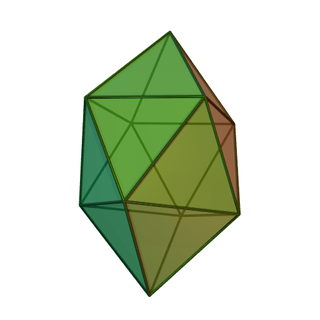
In geometry, the gyroelongated square bipyramid is a polyhedron with 16 triangular faces. it can be constructed from a square antiprism by attaching two equilateral square pyramids to each of its square faces. The same shape is also called hexakaidecadeltahedron, heccaidecadeltahedron, or tetrakis square antiprism; these last names mean a polyhedron with 16 triangular faces. It is an example of deltahedron, and of a Johnson solid.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

In geometry, a hexagonal trapezohedron or deltohedron is the fourth in an infinite series of trapezohedra which are dual polyhedra to the antiprisms. It has twelve faces which are congruent kites. It can be described by the Conway notation dA6.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

In geometry, a compound of two tetrahedra is constructed by two overlapping tetrahedra, usually implied as regular tetrahedra.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
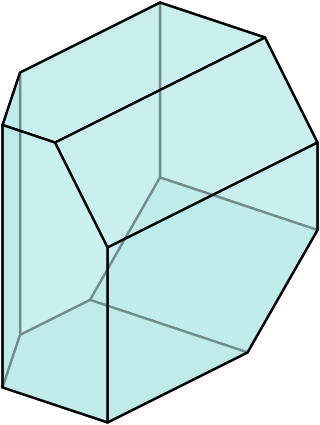
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.

In geometry, a diminished trapezohedron is a polyhedron in an infinite set of polyhedra, constructed by removing one of the polar vertices of a trapezohedron and replacing it by a new face (diminishment). It has one regular n-gonal base face, n triangle faces around the base, and n kites meeting on top. The kites can also be replaced by rhombi with specific proportions.








































