Spherical polyhedron

A familiar spherical polyhedron is the football, thought of as a spherical truncated icosahedron.

This beach ball would be a hosohedron with 6 spherical lune faces if the 2 white caps on the ends were removed.

In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons . A polyhedron whose vertices are equidistant from its center can be conveniently studied by projecting its edges onto the sphere to obtain a corresponding spherical polyhedron.

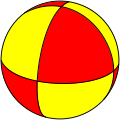
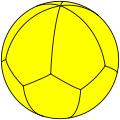
The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron.

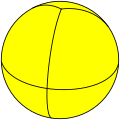
Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, {2, 6}, is a hosohedron, and {6, 2} is its dual dihedron.

History

During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) studied spherical polyhedra as part of a work on the geometry needed by craftspeople and architects. ^[1]

The work of Buckminster Fuller on geodesic domes in the mid 20th century triggered a boom in the study of spherical polyhedra. ^[2] At roughly the same time, Coxeter used them to enumerate all but one of the uniform polyhedra, through the construction of kaleidoscopes (Wythoff construction). ^[3]

Examples

All regular polyhedra, semiregular polyhedra, and their duals can be projected onto the sphere as tilings:

Schläfli symbol	{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Vertex config.	pq	q.2p.2p	p.q.p.q	p.2q.2q	qp	q.4.p.4	4.2q.2p	3.3.q.3.p
Tetrahedral symmetry (3 3 2)	33	3.6.6	3.3.3.3	3.6.6	33	3.4.3.4	4.6.6	3.3.3.3.3
		V3.6.6	V3.3.3.3	V3.6.6		V3.4.3.4	V4.6.6	V3.3.3.3.3
Octahedral symmetry (4 3 2)	43	3.8.8	3.4.3.4	4.6.6	34	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4	V4.6.8	V3.3.3.3.4
Icosahedral symmetry (5 3 2)	53	3.10.10	3.5.3.5	5.6.6	35	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.4	V4.6.10	V3.3.3.3.5
Dihedral example (p=6) (2 2 6)	62	2.12.12	2.6.2.6	6.4.4	26	2.4.6.4	4.4.12	3.3.3.6

Tiling of the sphere by spherical triangles (icosahedron with some of its spherical triangles distorted).

n	2	3	4	5	6	7	...
n-Prism (2 2 p)							...
n-Bipyramid (2 2 p)							...
n-Antiprism							...
n-Trapezohedron							...

Improper cases

Spherical tilings allow cases that polyhedra do not, namely hosohedra: figures as {2,n}, and dihedra: figures as {n,2}. Generally, regular hosohedra and regular dihedra are used.

Family of regular hosohedra · *n22 symmetry mutations of regular hosohedral tilings: nn

Space	Spherical						Euclidean
Tiling name	Henagonal hosohedron	Digonal hosohedron	Trigonal hosohedron	Square hosohedron	Pentagonal hosohedron	...	Apeirogonal hosohedron
Tiling image						...
Schläfli symbol	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	...	{2,∞}
Coxeter diagram						...
Faces and edges	1	2	3	4	5	...	∞
Vertices	2	2	2	2	2	...	2
Vertex config.	2	2.2	23	24	25	...	2∞

Family of regular dihedra · *n22 symmetry mutations of regular dihedral tilings: nn

Space	Spherical						Euclidean
Tiling name	Monogonal dihedron	Digonal dihedron	Trigonal dihedron	Square dihedron	Pentagonal dihedron	...	Apeirogonal dihedron
Tiling image						...
Schläfli symbol	{1,2}	{2,2}	{3,2}	{4,2}	{5,2}	...	{∞,2}
Coxeter diagram						...
Faces	2 {1}	2 {2}	2 {3}	2 {4}	2 {5}	...	2 {∞}
Edges and vertices	1	2	3	4	5	...	∞
Vertex config.	1.1	2.2	3.3	4.4	5.5	...	∞.∞

Relation to tilings of the projective plane

Spherical polyhedra having at least one inversive symmetry are related to projective polyhedra ^[4] (tessellations of the real projective plane) – just as the sphere has a 2-to-1 covering map of the projective plane, projective polyhedra correspond under 2-fold cover to spherical polyhedra that are symmetric under reflection through the origin.

The best-known examples of projective polyhedra are the regular projective polyhedra, the quotients of the centrally symmetric Platonic solids, as well as two infinite classes of even dihedra and hosohedra: ^[5]

• Hemi-cube, {4,3}/2
• Hemi-octahedron, {3,4}/2
• Hemi-dodecahedron, {5,3}/2
• Hemi-icosahedron, {3,5}/2
• Hemi-dihedron, {2p,2}/2, p≥1
• Hemi-hosohedron, {2,2p}/2, p≥1

See also

• Spherical geometry
• Spherical trigonometry
• Polyhedron
• Projective polyhedron
• Toroidal polyhedron
• Conway polyhedron notation

References

1. Sarhangi, Reza (September 2008). "Illustrating Abu al-Wafā' Būzjānī: Flat images, spherical constructions". Iranian Studies. 41 (4): 511–523. doi:10.1080/00210860802246184.
2. Popko, Edward S. (2012). Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press. p. xix. ISBN   978-1-4665-0430-1. Buckminster Fuller's invention of the geodesic dome was the biggest stimulus for spherical subdivision research and development.
3. Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. (1954). "Uniform polyhedra". Phil. Trans. 246 A (916): 401–50. JSTOR   91532.
4. McMullen, Peter; Schulte, Egon (2002). "6C. Projective Regular Polytopes". Abstract Regular Polytopes. Cambridge University Press. pp.  162–5. ISBN   0-521-81496-0.
5. Coxeter, H.S.M. (1969). "§21.3 Regular maps'". Introduction to Geometry (2nd ed.). Wiley. pp.  386–8. ISBN   978-0-471-50458-0. MR   0123930.