This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations .(November 2014) (Learn how and when to remove this template message) |
| Hemi-octahedron | |
|---|---|
 | |
| Type | abstract regular polyhedron globally projective polyhedron |
| Faces | 4 triangles |
| Edges | 6 |
| Vertices | 3 |
| Vertex configuration | 3.3.3.3 |
| Schläfli symbol | {3,4}/2 or {3,4}3 |
| Symmetry group | S4, order 24 |
| Dual polyhedron | hemicube |
| Properties | non-orientable Euler characteristic 1 |
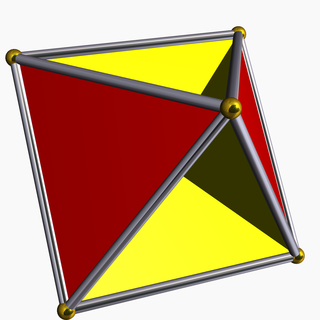
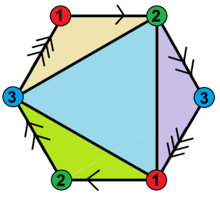
A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.
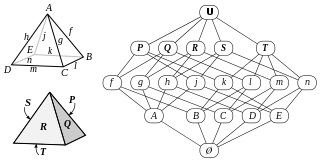
In mathematics, an abstract polytope is an algebraic partially ordered set or poset which captures the combinatorial properties of a traditional polytope, but not any purely geometric properties such as angles, edge lengths, etc.

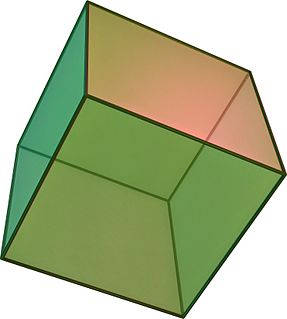
In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
Contents
It has 4 triangular faces, 6 edges, and 3 vertices. Its dual polyhedron is the hemicube.

In geometry, any polyhedron is associated with a second dual figure, where the vertices of one correspond to the faces of the other and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all are also geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
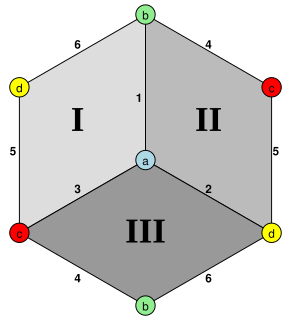
In abstract geometry, a hemicube is an abstract regular polyhedron, containing half the faces of a cube.
It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into four equal parts. It can be seen as a square pyramid without its base.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin.
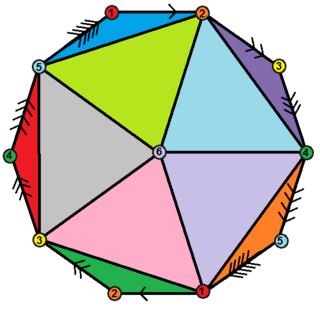
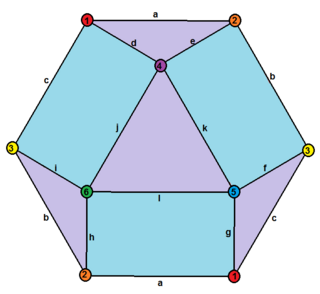
It can be represented symmetrically as a hexagonal or square Schlegel diagram:

In geometry, a Schlegel diagram is a projection of a polytope from into through a point just ouside one of its facets. The resulting entity is a polytopal subdivision of the facet in that, together with the original facet, is combinatorially equivalent to the original polytope. The diagram is named for Victor Schlegel, who in 1886 introduced this tool for studying combinatorial and topological properties of polytopes. In dimensions 3 and 4, a Schlegel diagram is a projection of a polyhedron into a plane figure and a projection of a 4-polytope to 3-space, respectively. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes.
It has an unexpected property that there are two distinct edges between every pair of vertices – any two vertices define a digon.
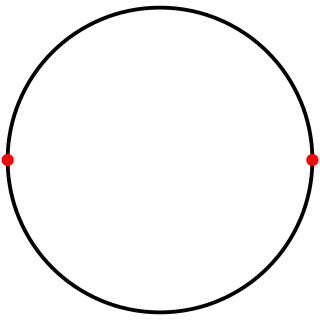
In geometry, a digon is a polygon with two sides (edges) and two vertices. Its construction is degenerate in a Euclidean plane because either the two sides would coincide or one or both would have to be curved; however, it can be easily visualised in elliptic space.