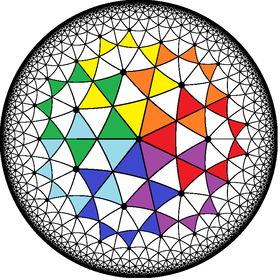
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
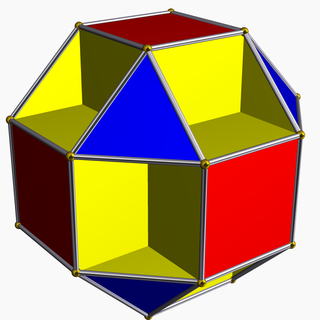
In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces (8 triangles, 6 squares, and 6 octagons), 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

In geometry, a heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex. It has Schläfli symbol of r{7,3}.
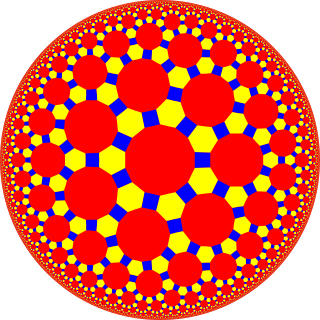
In geometry, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one square, one hexagon, and one tetradecagon (14-sides) on each vertex. It has Schläfli symbol of tr{7,3}.

In geometry, the truncated heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one triangle and two tetradecagons on each vertex. It has Schläfli symbol of t{7,3}. The tiling has a vertex configuration of 3.14.14.

In geometry, the rhombitriheptagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one heptagon, alternating between two squares. The tiling has Schläfli symbol rr{7, 3}. It can be seen as constructed as a rectified triheptagonal tiling, r{7,3}, as well as an expanded heptagonal tiling or expanded order-7 triangular tiling.
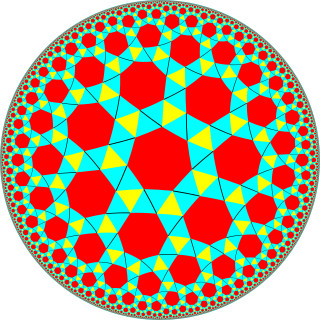
In geometry, the order-3 snub heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles and one heptagon on each vertex. It has Schläfli symbol of sr{7,3}. The snub tetraheptagonal tiling is another related hyperbolic tiling with Schläfli symbol sr{7,4}.

In geometry, the order-7 truncated triangular tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons. It has Schläfli symbol of t{3,7}.
In geometry, a vertex is a point where two or more curves, lines, or edges meet or intersect. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
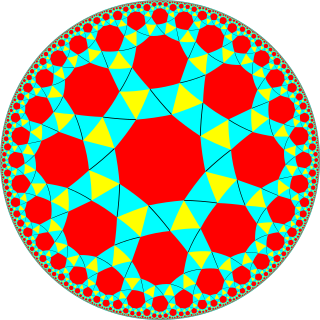
In geometry, the order-3 snub octagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangles, one octagon on each vertex. It has Schläfli symbol of sr{8,3}.

In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.

In geometry, the heptagrammic-order heptagonal tiling is a regular star-tiling of the hyperbolic plane. It has Schläfli symbol of {7,7/2}. The vertex figure heptagrams are {7/2}, . The heptagonal faces overlap with density 3.
In the geometry of hyperbolic 3-space, the order-7-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,7,3}.
In the geometry of hyperbolic 3-space, the order-infinite-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,∞,3}.