Related Research Articles

Giuseppe Peano was an Italian mathematician and glottologist. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in his honor. As part of this effort, he made key contributions to the modern rigorous and systematic treatment of the method of mathematical induction. He spent most of his career teaching mathematics at the University of Turin. He also wrote an international auxiliary language, Latino sine flexione, which is a simplified version of Classical Latin. Most of his books and papers are in Latino sine flexione, while others are in Italian.
Knowledge representation and reasoning is the field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can use to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology about how humans solve problems and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning, such as the application of rules or the relations of sets and subsets.
Logic programming is a programming, database and knowledge-representation and reasoning paradigm which is based on formal logic. A program, database or knowledge base in a logic programming language is a set of sentences in logical form, expressing facts and rules about some problem domain. Major logic programming language families include Prolog, Answer Set Programming (ASP) and Datalog. In all of these languages, rules are written in the form of clauses:
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions.
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th-century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete.

In theoretical computer science and mathematics, the theory of computation is the branch that deals with what problems can be solved on a model of computation, using an algorithm, how efficiently they can be solved or to what degree. The field is divided into three major branches: automata theory and formal languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".
Proof theory is a major branch of mathematical logic and theoretical computer science within which proofs are treated as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of a given logical system. Consequently, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature.

In artificial intelligence, symbolic artificial intelligence is the term for the collection of all methods in artificial intelligence research that are based on high-level symbolic (human-readable) representations of problems, logic and search. Symbolic AI used tools such as logic programming, production rules, semantic nets and frames, and it developed applications such as knowledge-based systems, symbolic mathematics, automated theorem provers, ontologies, the semantic web, and automated planning and scheduling systems. The Symbolic AI paradigm led to seminal ideas in search, symbolic programming languages, agents, multi-agent systems, the semantic web, and the strengths and limitations of formal knowledge and reasoning systems.
In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for (interactive) automated theorem proving. The first logical framework was Automath; however, the name of the idea comes from the more widely known Edinburgh Logical Framework, LF. Several more recent proof tools like Isabelle are based on this idea. Unlike a direct embedding, the logical framework approach allows many logics to be embedded in the same type system.
In artificial intelligence, a fluent is a condition that can change over time. In logical approaches to reasoning about actions, fluents can be represented in first-order logic by predicates having an argument that depends on time. For example, the condition "the box is on the table", if it can change over time, cannot be represented by ; a third argument is necessary to the predicate to specify the time: means that the box is on the table at time . This representation of fluents is modified in the situation calculus by using the sequence of the past actions in place of the current time.

Grammar induction is the process in machine learning of learning a formal grammar from a set of observations, thus constructing a model which accounts for the characteristics of the observed objects. More generally, grammatical inference is that branch of machine learning where the instance space consists of discrete combinatorial objects such as strings, trees and graphs.
Reification in natural language processing refers to where a natural language statement is transformed so actions and events in it become quantifiable variables. For example "John chased the duck furiously" can be transformed into something like

The following outline is provided as an overview of and topical guide to artificial intelligence:
In mathematical logic, the De Bruijn index is a tool invented by the Dutch mathematician Nicolaas Govert de Bruijn for representing terms of lambda calculus without naming the bound variables. Terms written using these indices are invariant with respect to α-conversion, so the check for α-equivalence is the same as that for syntactic equality. Each De Bruijn index is a natural number that represents an occurrence of a variable in a λ-term, and denotes the number of binders that are in scope between that occurrence and its corresponding binder. The following are some examples:
Statistical relational learning (SRL) is a subdiscipline of artificial intelligence and machine learning that is concerned with domain models that exhibit both uncertainty and complex, relational structure. Note that SRL is sometimes called Relational Machine Learning (RML) in the literature. Typically, the knowledge representation formalisms developed in SRL use first-order logic to describe relational properties of a domain in a general manner and draw upon probabilistic graphical models to model the uncertainty; some also build upon the methods of inductive logic programming. Significant contributions to the field have been made since the late 1990s.
Inductive programming (IP) is a special area of automatic programming, covering research from artificial intelligence and programming, which addresses learning of typically declarative and often recursive programs from incomplete specifications, such as input/output examples or constraints.
Ryszard S. Michalski was a Polish-American computer scientist. Michalski was Professor at George Mason University and a pioneer in the field of machine learning.
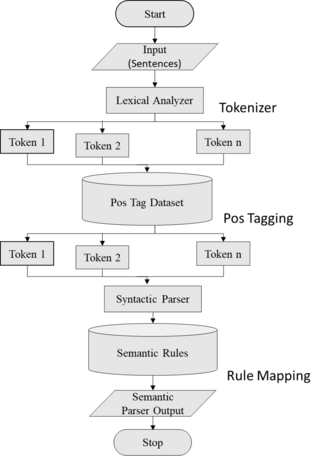
Semantic parsing is the task of converting a natural language utterance to a logical form: a machine-understandable representation of its meaning. Semantic parsing can thus be understood as extracting the precise meaning of an utterance. Applications of semantic parsing include machine translation, question answering, ontology induction, automated reasoning, and code generation. The phrase was first used in the 1970s by Yorick Wilks as the basis for machine translation programs working with only semantic representations. Semantic parsing is one of the important tasks in computational linguistics and natural language processing.
References
Michalski, R.S., "ATTRIBUTIONAL CALCULUS: A Logic and Representation Language for Natural Induction," Reports of the Machine Learning and Inference Laboratory, MLI 04–2, George Mason University, Fairfax, VA, April, 2004.