
In geometry, Barrow's inequality is an inequality relating the distances between an arbitrary point within a triangle, the vertices of the triangle, and certain points on the sides of the triangle. It is named after David Francis Barrow.

In geometry, Barrow's inequality is an inequality relating the distances between an arbitrary point within a triangle, the vertices of the triangle, and certain points on the sides of the triangle. It is named after David Francis Barrow.
Let P be an arbitrary point inside the triangle ABC. From P and ABC, define U, V, and W as the points where the angle bisectors of BPC, CPA, and APB intersect the sides BC, CA, AB, respectively. Then Barrow's inequality states that [1]
with equality holding only in the case of an equilateral triangle and P is the center of the triangle. [1]
Barrow's inequality can be extended to convex polygons. For a convex polygon with vertices let be an inner point and the intersections of the angle bisectors of with the associated polygon sides , then the following inequality holds: [2] [3]
Here denotes the secant function. For the triangle case the inequality becomes Barrow's inequality due to .

Barrow's inequality strengthens the Erdős–Mordell inequality, which has identical form except with PU, PV, and PW replaced by the three distances of P from the triangle's sides. It is named after David Francis Barrow. Barrow's proof of this inequality was published in 1937, as his solution to a problem posed in the American Mathematical Monthly of proving the Erdős–Mordell inequality. [1] This result was named "Barrow's inequality" as early as 1961. [4]
A simpler proof was later given by Louis J. Mordell. [5]

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.
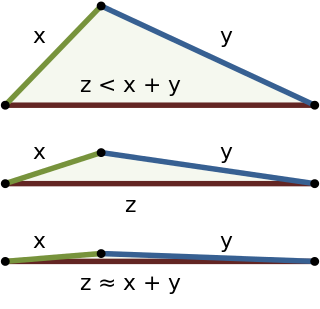
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If a, b, and c are the lengths of the sides of a triangle then the triangle inequality states that

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in -dimensional Euclidean space.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).

In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799, and is sometimes called the Wallace line.
In Euclidean geometry, the Erdős–Mordell inequality states that for any triangle ABC and point P inside ABC, the sum of the distances from P to the sides is less than or equal to half of the sum of the distances from P to the vertices. It is named after Paul Erdős and Louis Mordell. Erdős (1935) posed the problem of proving the inequality; a proof was provided two years later by Mordell and D. F. Barrow. This solution was however not very elementary. Subsequent simpler proofs were then found by Kazarinoff (1957), Bankoff (1958), and Alsina & Nelsen (2007).
The Erdős–Gallai theorem is a result in graph theory, a branch of combinatorial mathematics. It provides one of two known approaches to solving the graph realization problem, i.e. it gives a necessary and sufficient condition for a finite sequence of natural numbers to be the degree sequence of a simple graph. A sequence obeying these conditions is called "graphic". The theorem was published in 1960 by Paul Erdős and Tibor Gallai, after whom it is named.

In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.
An acute triangle is a triangle with three acute angles. An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle.
In graph theory, the graph removal lemma states that when a graph contains few copies of a given subgraph, then all of the copies can be eliminated by removing a small number of edges. The special case in which the subgraph is a triangle is known as the triangle removal lemma.