Related Research Articles

The travelling salesperson problem, also known as travelling salesman problem (TSP), asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements and objective are represented by linear relationships. Linear programming is a special case of mathematical programming.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

Dynamic programming is both a mathematical optimization method and an algorithmic paradigm. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

Hilbert's problems are 23 problems in mathematics published by German mathematician David Hilbert in 1900. They were all unsolved at the time, and several proved to be very influential for 20th-century mathematics. Hilbert presented ten of the problems at the Paris conference of the International Congress of Mathematicians, speaking on August 8 at the Sorbonne. The complete list of 23 problems was published later, in English translation in 1902 by Mary Frances Winston Newson in the Bulletin of the American Mathematical Society. Earlier publications appeared in Archiv der Mathematik und Physik.

Optimal control theory is a branch of control theory that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the Moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
Global optimization is a branch of applied mathematics and numerical analysis that attempts to find the global minima or maxima of a function or a set of functions on a given set. It is usually described as a minimization problem because the maximization of the real-valued function is equivalent to the minimization of the function .

Max Wilhelm Dehn was a German mathematician most famous for his work in geometry, topology and geometric group theory. Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States.

Richard Ernest Bellman was an American applied mathematician, who introduced dynamic programming in 1953, and made important contributions in other fields of mathematics, such as biomathematics. He founded the leading biomathematical journal Mathematical Biosciences.
The Hamilton-Jacobi-Bellman (HJB) equation is a nonlinear partial differential equation that provides necessary and sufficient conditions for optimality of a control with respect to a loss function. Its solution is the value function of the optimal control problem which, once known, can be used to obtain the optimal control by taking the maximizer of the Hamiltonian involved in the HJB equation.
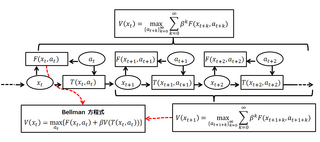
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
Joseph Bishop Keller was an American mathematician who specialized in applied mathematics. He was best known for his work on the "geometrical theory of diffraction" (GTD).
In mathematics, the moving sofa problem or sofa problem is a two-dimensional idealisation of real-life furniture-moving problems and asks for the rigid two-dimensional shape of largest area that can be maneuvered through an L-shaped planar region with legs of unit width. The area thus obtained is referred to as the sofa constant. The exact value of the sofa constant is an open problem. The currently leading solution, by Joseph L. Gerver, has a value of approximately 2.2195 and is thought to be close to the optimal, based upon subsequent study and theoretical bounds.
In computational complexity theory, the linear search problem is an optimal search problem introduced by Richard E. Bellman and independently considered by Anatole Beck.
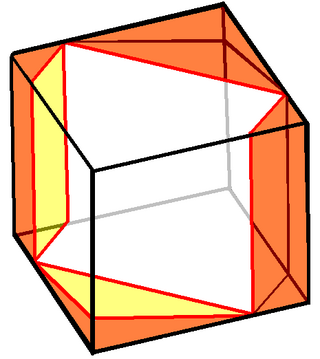
In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into two pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in 2000. The Clay Institute has pledged a US$1 million prize for the first correct solution to each problem.
Moser's worm problem is an unsolved problem in geometry formulated by the Austrian-Canadian mathematician Leo Moser in 1966. The problem asks for the region of smallest area that can accommodate every plane curve of length 1. Here "accommodate" means that the curve may be rotated and translated to fit inside the region. In some variations of the problem, the region is restricted to be convex.

In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.

In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
References
- ↑ Bellman, R. (1956). "Minimization problem". Research problems. Bulletin of the American Mathematical Society . 62 (3): 270. doi: 10.1090/S0002-9904-1956-10021-9 .
- ↑ Finch, S. R.; Wetzel, J. E. (2004). "Lost in a forest" (PDF). American Mathematical Monthly . 11 (8): 645–654. doi:10.2307/4145038. JSTOR 4145038. MR 2091541.
- ↑ Williams, S. W. (2000). "Million buck problems" (PDF). National Association of Mathematicians Newsletter. 31 (2): 1–3.
- ↑ Ward, John W. (2008). "Exploring the Bellman Forest Problem" (PDF). Retrieved 2020-12-14.