Bernstein's theorem (polynomials)

Last updated November 02, 2020

Bernstein's theorem is an inequality relating the maximum modulus of a complex polynomial function on the unit disk with the maximum modulus of its derivative on the unit disk. It was proven by Sergei Bernstein while he was working on approximation theory.^[1]

Statement

Let $\max _{|z|=1}|f(z)|$ denote the maximum modulus of an arbitrary function $f(z)$ on $|z|=1$ , and let $f'(z)$ denote its derivative. Then for every polynomial $P(z)$ of degree $n$ we have

\max _{|z|=1}|P'(z)|\leq n\max _{|z|=1}|P(z)|

.

The inequality is best possible with equality holding if and only if

P(z)=\alpha z^{n},\ |\alpha |=\max _{|z|=1}|P(z)|

.

^[2]

Proof

Let $P(z)$ be a polynomial of degree $n$ , and let $Q(z)$ be another polynomial of the same degree with no zeros in $|z|\geq 1$ . We show first that if $|P(z)|<|Q(z)|$ on $|z|=1$ , then $|P'(z)|<|Q'(z)|$ on $|z|\geq 1$ .

By Rouché's theorem, $P(z)+\varepsilon \ Q(z)$ with $|\varepsilon |\geq 1$ has all its zeros in $|z|<1$ . By virtue of the Gauss–Lucas theorem, $P'(z)+\varepsilon \ Q'(z)$ has all its zeros in $|z|<1$ as well. It follows that $|P'(z)|<|Q'(z)|$ on $|z|\geq 1$ , otherwise we could choose an $\varepsilon$ with $|\varepsilon |\geq 1$ such that $P'(z)+\varepsilon Q'(z)$ has a zero in $|z|\geq 1$ .

For an arbitrary polynomial $P(z)$ of degree $n$ , we obtain Bernstein's Theorem by applying the above result to the polynomials $Q(z)=Cz^{n}$ , where $C$ is an arbitrary constant exceeding $\max _{|z|=1}|P(z)|$ .

Bernstein's inequality

In mathematical analysis, Bernstein's inequality states that on the complex plane, within the disk of radius 1, the degree of a polynomial times the maximum value of a polynomial is an upper bound for the similar maximum of its derivative. Taking the k-th derivative of the theorem,

\max _{|z|\leq 1}(|P^{(k)}(z)|)\leq {\frac {n!}{(n-k)!}}\cdot \max _{|z|\leq 1}(|P(z)|).

Similar results

Paul Erdős conjectured that if $P(z)$ has no zeros in $|z|<1$ , then $\max _{|z|=1}|P'(z)|\leq {\frac {n}{2}}\max _{|z|=1}|P(z)|$ . This was proved by Peter Lax.^[3]

M. A. Malik showed that if $P(z)$ has no zeros in $|z|<k$ for a given $k\geq 1$ , then $\max _{|z|=1}|P'(z)|\leq {\frac {n}{1+k}}\max _{|z|=1}|P(z)|$ .^[4]

Related Research Articles

In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.

In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

In number theory, a Liouville number is a real number x with the property that, for every positive integer n, there exist infinitely many pairs of integers with q > 1 such that

In probability theory, Chebyshev's inequality guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/k² of the distribution's values can be more than k standard deviations away from the mean. The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers.

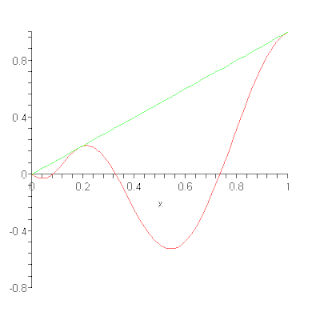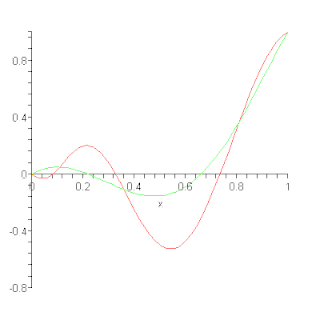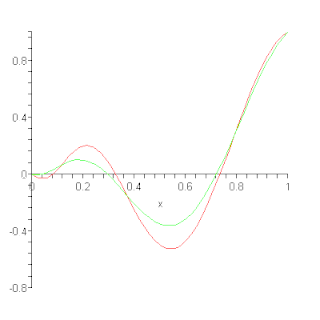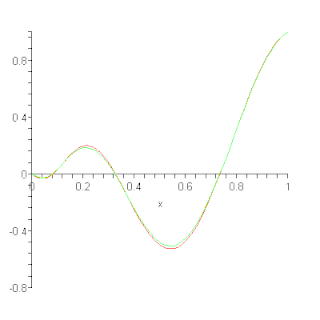
In the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials.

In probability theory, the Chernoff bound, named after Herman Chernoff but due to Herman Rubin, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is a sharper bound than the known first- or second-moment-based tail bounds such as Markov's inequality or Chebyshev's inequality, which only yield power-law bounds on tail decay. However, the Chernoff bound requires that the variates be independent – a condition that neither Markov's inequality nor Chebyshev's inequality require, although Chebyshev's inequality does require the variates to be pairwise independent.

In mathematics, Roth's theorem is a fundamental result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that algebraic numbers cannot have many rational number approximations that are 'very good'. Over half a century, the meaning of very good here was refined by a number of mathematicians, starting with Joseph Liouville in 1844 and continuing with work of Axel Thue (1909), Carl Ludwig Siegel (1921), Freeman Dyson (1947), and Klaus Roth (1955).

In probability theory, Hoeffding's inequality provides an upper bound on the probability that the sum of bounded independent random variables deviates from its expected value by more than a certain amount. Hoeffding's inequality was proven by Wassily Hoeffding in 1963.

In measure theory, an area of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is also named Severini–Egoroff theorem or Severini–Egorov theorem, after Carlo Severini, an Italian mathematician, and Dmitri Egorov, a Russian physicist and geometer, who published independent proofs respectively in 1910 and 1911.

In mathematics, there are at least two results known as Weyl's inequality.

In probability theory, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X₁, ..., X_n be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive $,$

In mathematics, a univariate polynomial of degree $n$ with real or complex coefficients has $n$ complex roots, if counted with their multiplicities. They form a set of $n$ points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.

Anatoly Alexeyevich Karatsuba was a Russian mathematician working in the field of analytic number theory, p-adic numbers and Dirichlet series.

Uniform convergence in probability is a form of convergence in probability in statistical asymptotic theory and probability theory. It means that, under certain conditions, the empirical frequencies of all events in a certain event-family converge to their theoretical probabilities. Uniform convergence in probability has applications to statistics as well as machine learning as part of statistical learning theory.

The exponential mechanism is a technique for designing differentially private algorithms. It was developed by Frank McSherry and Kunal Talwar in 2007. Their work was recognized as a co-winner of the 2009 PET Award for Outstanding Research in Privacy Enhancing Technologies.

In complex analysis and geometric function theory, the Grunsky matrices, or Grunsky operators, are infinite matrices introduced in 1939 by Helmut Grunsky. The matrices correspond to either a single holomorphic function on the unit disk or a pair of holomorphic functions on the unit disk and its complement. The Grunsky inequalities express boundedness properties of these matrices, which in general are contraction operators or in important special cases unitary operators. As Grunsky showed, these inequalities hold if and only if the holomorphic function is univalent. The inequalities are equivalent to the inequalities of Goluzin, discovered in 1947. Roughly speaking, the Grunsky inequalities give information on the coefficients of the logarithm of a univalent function; later generalizations by Milin, starting from the Lebedev–Milin inequality, succeeded in exponentiating the inequalities to obtain inequalities for the coefficients of the univalent function itself. The Grunsky matrix and its associated inequalities were originally formulated in a more general setting of univalent functions between a region bounded by finitely many sufficiently smooth Jordan curves and its complement: the results of Grunsky, Goluzin and Milin generalize to that case.

In mathematics, singular integral operators of convolution type are the singular integral operators that arise on Rⁿ and Tⁿ through convolution by distributions; equivalently they are the singular integral operators that commute with translations. The classical examples in harmonic analysis are the harmonic conjugation operator on the circle, the Hilbert transform on the circle and the real line, the Beurling transform in the complex plane and the Riesz transforms in Euclidean space. The continuity of these operators on L² is evident because the Fourier transform converts them into multiplication operators. Continuity on L^p spaces was first established by Marcel Riesz. The classical techniques include the use of Poisson integrals, interpolation theory and the Hardy–Littlewood maximal function. For more general operators, fundamental new techniques, introduced by Alberto Calderón and Antoni Zygmund in 1952, were developed by a number of authors to give general criteria for continuity on L^p spaces. This article explains the theory for the classical operators and sketches the subsequent general theory.

In mathematics, a uniformly smooth space is a normed vector space $satisfying the property that for every there exists such that if with and then$

In mathematics, Young's inequality for products is a mathematical inequality about the product of two numbers. The inequality is named after William Henry Young and should not be confused with Young's convolution inequality.

Wiman-Valiron theory is a mathematical theory invented by Anders Wiman as a tool to study the behavior of arbitrary entire functions. After the work of Wiman, the theory was developed by other mathematicians, and extended to more general classes of analytic functions. The main result of the theory is an asymptotic formula for the function and its derivatives near the point where the maximum modulus of this function is attained.

References

↑ R. P. Boas, Jr., Inequalities for the derivatives of polynomials, Math. Mag. 42 (1969), 165–174.
↑ M. A. Malik, M. C. Vong, Inequalities concerning the derivative of polynomials, Rend. Circ. Mat. Palermo (2) 34 (1985), 422–426.
↑ P. D. Lax, Proof of a conjecture of P. Erdös on the derivative of a polynomial, Bull. Amer. Math. Soc. 50 (1944), 509–513.
↑ M. A. Malik, On the derivative of a polynomial J. London Math. Soc (2) 1 (1969), 57–60.