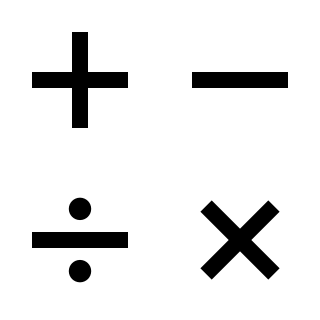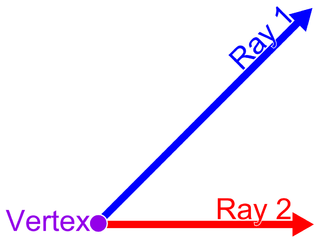
In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.
In mathematics, a binary relation between two sets A and B is a set of ordered pairs consisting of elements a of A and elements b of B; in short, it is a subset of the Cartesian product A × B. It encodes the information of relation: an element a is related to an element b if and only if the pair belongs to the set.
In mathematics, a finitary relation is a property that assigns truth values to finite tuples of elements. Typically, the property describes a possible connection between the components of a k-tuple. For a given set of k-tuples, a truth value is assigned to each k-tuple according to whether the property does or does not hold. When k = 2, one has the most common version, a binary relation.
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.
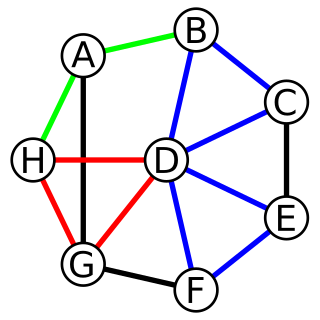
In graph theory, a cycle is a path of edges and vertices wherein a vertex is reachable from itself.
There are several different types of cycles, principally a closed walk and a simple cycle; also, e.g., an element of the cycle space of the graph.
If a graph contains no cycles it is referred to as being acyclic.
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b and b is related to an element c then a is also related to c. Transitivity is a key property of both partial order relations and equivalence relations.
A binary code represents text, computer processor instructions, or any other data using a two-symbol system. The two-symbol system used is often "0" and "1" from the binary number system. The binary code assigns a pattern of binary digits, also known as bits, to each character, instruction, etc. For example, a binary string of eight bits can represent any of 256 possible values and can, therefore, represent a wide variety of different items.

In mathematics and digital electronics, a binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically "0" (zero) and "1" (one).

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it ; such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations such as the multiplication and addition of numbers are commutative, was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A corresponding property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.

The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24. It is notable for having a revolutionary impact on the field of number theory as it not only turned the field truly rigorous and systematic but also paved the path for modern number theory. In this book Gauss brought together and reconciled results in number theory obtained by mathematicians such as Fermat, Euler, Lagrange, and Legendre and added many profound and original results of his own.
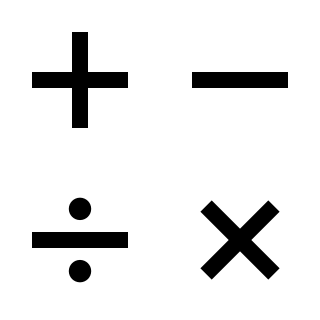
In mathematics, an operation is a calculation from zero or more input values to an output value. The number of operands is the arity of the operation. The most commonly studied operations are binary operations, such as addition and multiplication, and unary operations, such as additive inverse and multiplicative inverse. An operation of arity zero, or nullary operation, is a constant. The mixed product is an example of an operation of arity 3, also called ternary operation. Generally, the arity is supposed to be finite. However, infinitary operations are sometimes considered, in which context the "usual" operations of finite arity are called finitary operations.
Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. It includes everything from elementary equation solving to the study of abstractions such as groups, rings, and fields. The more basic parts of algebra are called elementary algebra; the more abstract parts are called abstract algebra or modern algebra. Elementary algebra is generally considered to be essential for any study of mathematics, science, or engineering, as well as such applications as medicine and economics. Abstract algebra is a major area in advanced mathematics, studied primarily by professional mathematicians.

In algebra, which is a broad division of mathematics, abstract algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras. The term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra.
A Schröder–Bernstein property is any mathematical property that matches the following pattern
In mathematical invariant theory, an invariant of a binary form is a polynomial in the coefficients of a binary form in two variables x and y that remains invariant under the special linear group acting on the variables x and y.
In mathematical invariant theory, the catalecticant of a form of even degree is a polynomial in its coefficients that vanishes when the form is a sum of an unusually small number of powers of linear forms. It was introduced by Sylvester (1852); see Miller (2010). The word catalectic refers to an incomplete line of verse, lacking a syllable at the end or ending with an incomplete foot.
In mathematical invariant theory, a perpetuant is informally an irreducible covariant of a form or infinite degree. More precisely, the dimension of the space of irreducible covariants of given degree and weight for a binary form stabilizes provided the degree of the form is larger than the weight of the covariant, and the elements of this space are called perpetuants. Perpetuants were introduced and named by Sylvester (1882, p.105). MacMahon and Stroh (1888) classified the perpetuants. Elliott (1907) describes the early history of perpetuants and gives an annotated bibliography. There are very few papers after about 1910 discussing perpetuants; is one of the few exceptions.
In mathematics, a ternary quartic form is a degree 4 homogeneous polynomial in three variables.