Area is the quantity that expresses the extent of a two-dimensional figure or shape or planar lamina, in the plane. Surface area is its analog on the two-dimensional surface of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve or the volume of a solid.
In geometry, the circumference is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the locus corresponding to the edge of a disk.
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.
A perimeter is a path that encompasses/surrounds a two-dimensional shape. The term may be used either for the path, or its length—in one dimension. It can be thought of as the length of the outline of a shape. The perimeter of a circle or ellipse is called its circumference.
A sphere is a geometrical object in three-dimensional space that is the surface of a ball.
A right triangle or right-angled triangle is a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry.
In geometry, an equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,
In geometry, a curve of constant width is a convex planar shape whose width is the same regardless of the orientation of the curve.
In geometry, the area enclosed by a circle of radius r is π r2. Here the Greek letter π represents a constant, approximately equal to 3.14159, which is equal to the ratio of the circumference of any circle to its diameter.
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also a slower-paced Introduction to systolic geometry.
In differential geometry, Pu's inequality, proved by Pao Ming Pu, relates the area of an arbitrary Riemannian surface homeomorphic to the real projective plane with the lengths of the closed curves contained in it.
In geometry, a bicentric polygon is a tangential polygon which is also cyclic — that is, inscribed in an outer circle that passes through each vertex of the polygon. All triangles and all regular polygons are bicentric. On the other hand, a rectangle with unequal sides is not bicentric, because no circle can be tangent to all four sides.
Systolic geometry is a branch of differential geometry, a field within mathematics, studying problems such as the relationship between the area inside a closed curve C, and the length or perimeter of C. Since the area A may be small while the length l is large, when C looks elongated, the relationship can only take the form of an inequality. What is more, such an inequality would be an upper bound for A: there is no interesting lower bound just in terms of the length.
Liu Hui's π algorithm was invented by Liu Hui, a mathematician of the Cao Wei Kingdom. Before his time, the ratio of the circumference of a circle to its diameter was often taken experimentally as three in China, while Zhang Heng (78–139) rendered it as 3.1724 or as . Liu Hui was not satisfied with this value. He commented that it was too large and overshot the mark. Another mathematician Wan Fan (219–257) provided π ≈ 142/45 ≈ 3.156. All these empirical π values were accurate to two digits. Liu Hui was the first Chinese mathematician to provide a rigorous algorithm for calculation of π to any accuracy. Liu Hui's own calculation with a 96-gon provided an accuracy of five digits: π ≈ 3.1416.
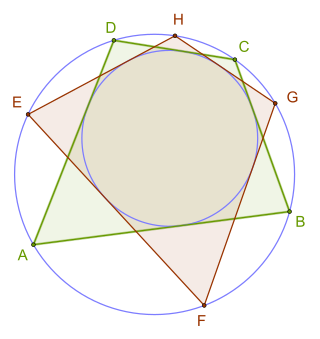
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and center of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.
In Euclidean geometry, a right kite is a kite that can be inscribed in a circle. That is, it is a kite with a circumcircle. Thus the right kite is a convex quadrilateral and has two opposite right angles. If there are exactly two right angles, each must be between sides of different lengths. All right kites are bicentric quadrilaterals, since all kites have an incircle. One of the diagonals divides the right kite into two right triangles and is also a diameter of the circumcircle.
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle.
