Candido's identity, named after the Italian mathematician Giacomo Candido, is an identity for real numbers. It states that for two arbitrary real numbers and the following equality holds: [2]
The identity however is not restricted to real numbers but holds in every commutative ring. [2]
Candido originally devised the identity to prove the following identity for Fibonacci numbers: [1]
A straightforward algebraic proof can be attained by simply completely expanding both sides of the equation. The identity however can also be interpreted geometrically. In this case it states that the area of square with side length equals twice the sum of areas of three squares with side lengths , and . This allows for the following proof due to Roger B. Nelsen: [3]
.
In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the sequence begins
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is
In algebra, the Brahmagupta–Fibonacci identity expresses the product of two sums of two squares as a sum of two squares in two different ways. Hence the set of all sums of two squares is closed under multiplication. Specifically, the identity says
In arithmetic and algebra, the cube of a number n is its third power, that is, the result of multiplying three instances of n together. The cube of a number or any other mathematical expression is denoted by a superscript 3, for example 23 = 8 or (x + 1)3.
In mathematics, the Fibonacci polynomials are a polynomial sequence which can be considered as a generalization of the Fibonacci numbers. The polynomials generated in a similar way from the Lucas numbers are called Lucas polynomials.
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.
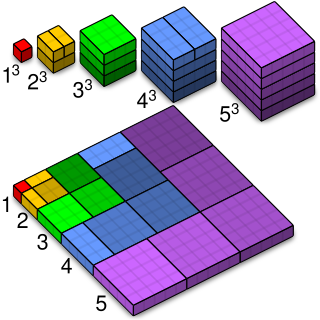
In number theory, the sum of the first n cubes is the square of the nth triangular number. That is,
In Euclidean geometry, Ptolemy's inequality relates the six distances determined by four points in the plane or in a higher-dimensional space. It states that, for any four points A, B, C, and D, the following inequality holds:
In mathematics, the infinite series 1/4 + 1/16 + 1/64 + 1/256 + ⋯ is an example of one of the first infinite series to be summed in the history of mathematics; it was used by Archimedes circa 250–200 BC. As it is a geometric series with first term 1/4 and common ratio 1/4, its sum is
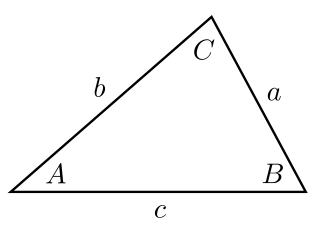
In mathematics, Weitzenböck's inequality, named after Roland Weitzenböck, states that for a triangle of side lengths , , , and area , the following inequality holds:
In Euclidean geometry, the Erdős–Mordell inequality states that for any triangle ABC and point P inside ABC, the sum of the distances from P to the sides is less than or equal to half of the sum of the distances from P to the vertices. It is named after Paul Erdős and Louis Mordell. Erdős (1935) posed the problem of proving the inequality; a proof was provided two years later by Mordell and D. F. Barrow. This solution was however not very elementary. Subsequent simpler proofs were then found by Kazarinoff (1957), Bankoff (1958), and Alsina & Nelsen (2007).
In mathematics, a proof without words is an illustration of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than formal or mathematically rigorous proofs due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable.
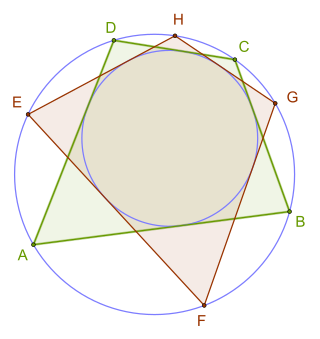
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.
Fermat's right triangle theorem is a non-existence proof in number theory, published in 1670 among the works of Pierre de Fermat, soon after his death. It is the only complete proof given by Fermat. It has many equivalent formulations, one of which was stated in 1225 by Fibonacci. In its geometric forms, it states:
In Euclidean geometry the Newton line is the line that connects the midpoints of the two diagonals in a convex quadrilateral with at most two parallel sides.
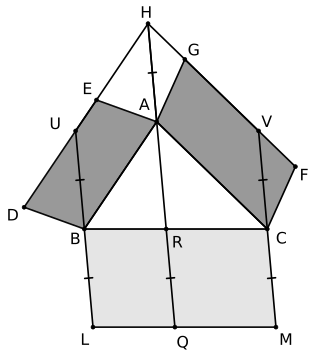
Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.
Giacomo Candido was an Italian mathematician and historian of mathematics.
Van Schooten's theorem, named after the Dutch mathematician Frans van Schooten, describes a property of equilateral triangles. It states:
Proofs That Really Count: the Art of Combinatorial Proof is an undergraduate-level mathematics book on combinatorial proofs of mathematical identies. That is, it concerns equations between two integer-valued formulas, shown to be equal either by showing that both sides of the equation count the same type of mathematical objects, or by finding a one-to-one correspondence between the different types of object that they count. It was written by Arthur T. Benjamin and Jennifer Quinn, and published in 2003 by the Mathematical Association of America as volume 27 of their Dolciani Mathematical Expositions series. It won the Beckenbach Book Prize of the Mathematical Association of America.
The median triangle of a given (reference) triangle is a triangle, the sides of which are equal and parallel to the medians of its reference triangle. The area of the median triangle is of the area of its reference triangle, and the median triangle of the median triangle is similar to the reference triangle of the first median triangle with a scaling factor of .
