See also
| This disambiguation page lists articles associated with the title Canonical model. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
Canonical model may refer to:
A canonical model is a design pattern used to communicate between different data formats. Essentially: create a data model which is a superset of all the others ("canonical"), and create a "translator" module or layer to/from which all existing modules exchange data with other modules. The individual modules can then be considered endpoints on an intelligent bus; the bus centralises all the data-translation intelligence.
In mathematics, the pluricanonical ring of an algebraic variety V, or of a complex manifold, is the graded ring
In mathematics, the relative canonical model of a singular variety is a particular canonical variety that maps to , which simplifies the structure. The precise definition is:
| This disambiguation page lists articles associated with the title Canonical model. If an internal link led you here, you may wish to change the link to point directly to the intended article. |

Saul Aaron Kripke is an American philosopher and logician. He is a Distinguished Professor of Philosophy at the Graduate Center of the City University of New York and emeritus professor at Princeton University. Since the 1960s, Kripke has been a central figure in a number of fields related to mathematical logic, philosophy of language, philosophy of mathematics, metaphysics, epistemology, and set theory. Much of his work remains unpublished or exists only as tape recordings and privately circulated manuscripts. Kripke was the recipient of the 2001 Schock Prize in Logic and Philosophy.

Emil Leon Post was an American mathematician and logician. He is best known for his work in the field that eventually became known as computability theory.

In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. The distinction between "canonical" and "normal" forms varies by subfield. In most fields, a canonical form specifies a unique representation for every object, while a normal form simply specifies its form, without the requirement of uniqueness.
In mathematics, the canonical bundle of a non-singular algebraic variety of dimension over a field is the line bundle , which is the nth exterior power of the cotangent bundle Ω on V.

Shigefumi Mori is a Japanese mathematician, known for his work in algebraic geometry, particularly in relation to the classification of three-folds.
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke.
In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the heat bath, so that the states of the system will differ in total energy.
In algebraic geometry, the Kodaira dimension κ(X) measures the size of the canonical model of a projective variety X.
In mathematical logic, a theory is complete if, for every formula in the theory's language, that formula or its negation is demonstrable. Recursively axiomatizable first-order theories that are rich enough to allow general mathematical reasoning to be formulated cannot be complete, as demonstrated by Gödel's first incompleteness theorem.
In algebraic geometry, flips and flops are codimension-2 surgery operations arising in the minimal model program, given by blowing up along a relative canonical ring. In dimension 3 flips are used to construct minimal models, and any two birationally equivalent minimal models are connected by a sequence of flops. It is conjectured that the same is true in higher dimensions.
Donald Marolf is a theoretical physicist, and currently a Professor of Physics, and head of the physics department at the University of California, Santa Barbara.
In algebraic geometry, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible. The subject has its origins in the classical birational geometry of surfaces studied by the Italian school, and is currently an active research area within algebraic geometry.
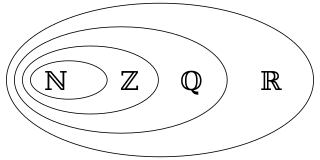
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
In algebraic geometry, a crepant resolution of a singularity is a resolution that does not affect the canonical class of the manifold. The term "crepant" was coined by Miles Reid (1983) by removing the prefix "dis" from the word "discrepant", to indicate that the resolutions have no discrepancy in the canonical class.
In mathematics, canonical singularities appear as singularities of the canonical model of a projective variety, and terminal singularities are special cases that appear as singularities of minimal models. They were introduced by Reid (1980). Terminal singularities are important in the minimal model program because smooth minimal models do not always exist, and thus one must allow certain singularities, namely the terminal singularities.
In computational mathematics, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes exact computation with expressions containing variables that have no given value and are manipulated as symbols.
Caucher Birkar is a UK-based Iranian Kurdish mathematician and a professor at the University of Cambridge.