Characteristic set may refer to
 | This disambiguation page lists mathematics articles associated with the same title. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not usually produce an optimal solution, but nonetheless, a greedy heuristic may yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension. Specifically, it is defined as the largest cardinality of an algebraically independent subset of L over K.
In abstract algebra, a subset of a field is algebraically independent over a subfield if the elements of do not satisfy any non-trivial polynomial equation with coefficients in .
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is called a planar matroid; these are exactly the graphic matroids formed from planar graphs.
In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc.. These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.
In mathematics, a regular matroid is a matroid that can be represented over all fields.
In the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle.
In the mathematics of matroids and lattices, a geometric lattice is a finite atomistic semimodular lattice, and a matroid lattice is an atomistic semimodular lattice without the assumptions of finiteness. Geometric lattices and matroid lattices, respectively, form the lattices of flats of finite and infinite matroids, and every geometric or matroid lattice comes from a matroid in this way.
In combinatorial optimization, the matroid intersection problem is to find a largest common independent set in two matroids over the same ground set. If the elements of the matroid are assigned real weights, the weighted matroid intersection problem is to find a common independent set with the maximum possible weight. These problems generalize many problems in combinatorial optimization including finding maximum matchings and maximum weight matchings in bipartite graphs and finding arborescences in directed graphs.
In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.
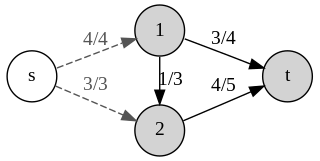
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.
Rota's excluded minors conjecture is one of a number of conjectures made by mathematician Gian-Carlo Rota. It is considered to be an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture has been announced by Geelen, Gerards, and Whittle.
In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.
In the mathematical theory of matroids, the rank of a matroid is the maximum size of an independent set in the matroid. The rank of a subset S of elements of the matroid is, similarly, the maximum size of an independent subset of S, and the rank function of the matroid maps sets of elements to their ranks.
In mathematics, an algebraic matroid is a matroid, a combinatorial structure, that expresses an abstraction of the relation of algebraic independence.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.