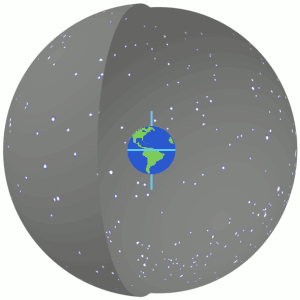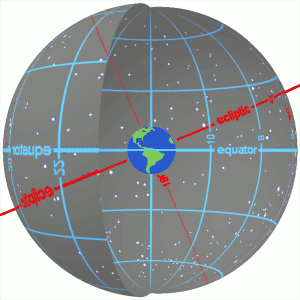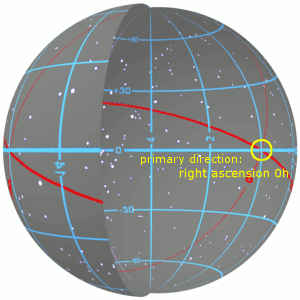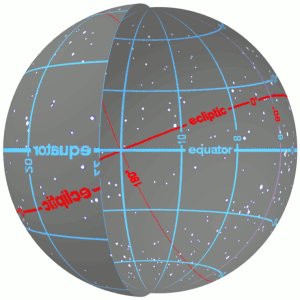
In astronomy, declination is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question.

Longitude, is a geographic coordinate that specifies the east–west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians connect points with the same longitude. By convention, one of these, the Prime Meridian, which passes through the Royal Observatory, Greenwich, England, was allocated the position of 0° longitude. The longitude of other places is measured as the angle east or west from the Prime Meridian, ranging from 0° at the Prime Meridian to +180° eastward and −180° westward. Specifically, it is the angle between a plane through the Prime Meridian and a plane through both poles and the location in question.

Right ascension is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the point above the earth in question. When paired with declination, these astronomical coordinates specify the direction of a point on the celestial sphere in the equatorial coordinate system.

A geographic coordinate system is a coordinate system that enables every location on Earth to be specified by a set of numbers, letters or symbols. The coordinates are often chosen such that one of the numbers represents a vertical position and two or three of the numbers represent a horizontal position; alternatively, a geographic position may be expressed in a combined three-dimensional Cartesian vector. A common choice of coordinates is latitude, longitude and elevation. To specify a location on a plane requires a map projection.

The ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions and orbits of Solar System objects. Because most planets and many small Solar System bodies have orbits with slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the vernal (northward) equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates.

The galactic coordinate system is a celestial coordinate system in spherical coordinates, with the Sun as its center, the primary direction aligned with the approximate center of the Milky Way galaxy, and the fundamental plane parallel to an approximation of the galactic plane but offset to its north. It uses the right-handed convention, meaning that coordinates are positive toward the north and toward the east in the fundamental plane.
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability.

A gravitational singularity, spacetime singularity or simply singularity is a location in spacetime where the gravitational field of a celestial body becomes infinite in a way that does not depend on the coordinate system. The quantities used to measure gravitational field strength are the scalar invariant curvatures of spacetime, which includes a measure of the density of matter. Since such quantities become infinite within the singularity, the laws of normal spacetime cannot exist.

A Brief History of Time: From the Big Bang to Black Holes is a popular-science book on cosmology by British physicist Stephen Hawking. It was first published in 1988. Hawking wrote the book for nonspecialist readers with no prior knowledge of scientific theories.

The Ordnance Survey National Grid reference system is a system of geographic grid references used in Great Britain, distinct from latitude and longitude. It is often called British National Grid (BNG).

A (geographic) meridian is the half of an imaginary great circle on the Earth's surface, terminated by the North Pole and the South Pole, connecting points of equal longitude, as measured in angular degrees east or west of the Prime Meridian. The position of a point along the meridian is given by that longitude and its latitude, measured in angular degrees north or south of the Equator. Each meridian is perpendicular to all circles of latitude. Each is also the same length, being half of a great circle on the Earth's surface and therefore measuring 20,003.93 km.
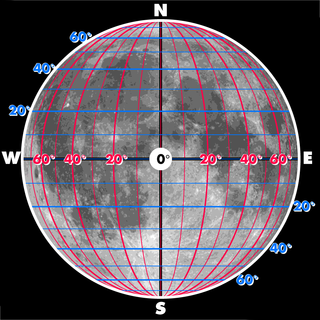
Selenographic coordinates are used to refer to locations on the surface of Earth's moon. Any position on the lunar surface can be referenced by specifying two numerical values, which are comparable to the latitude and longitude of Earth. The longitude gives the position east or west of the Moon's prime meridian, which is the line passing from the lunar north pole through the point on the lunar surface directly facing Earth to the lunar south pole. This can be thought of as the midpoint of the visible Moon as seen from the Earth. The latitude gives the position north or south of the lunar equator. Both of these coordinates are given in degrees.

The longitude of the ascending node is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a reference direction, called the origin of longitude, to the direction of the ascending node, measured in a reference plane. The ascending node is the point where the orbit of the object passes through the plane of reference, as seen in the adjacent image. Commonly used reference planes and origins of longitude include:
In theoretical physics, the Hartle–Hawking state, named after James Hartle and Stephen Hawking, is a proposal concerning the state of the Universe prior to the Planck epoch.
The World Geographic Reference System (GEOREF) is a grid-based method of specifying locations on the surface of the Earth. GEOREF is essentially based on the geographic system of latitude and longitude, but using a simpler and more flexible notation. GEOREF was used primarily for air navigation, particularly in military or inter-service applications, but it is rarely seen today. However, GEOREF can be used with any map or chart that has latitude and longitude printed on it.
The n-vector representation is a three-parameter non-singular representation well-suited for replacing latitude and longitude as horizontal position representation in mathematical calculations and computer algorithms.

Stephen William Hawking was an English theoretical physicist, cosmologist, and author who was director of research at the Centre for Theoretical Cosmology at the University of Cambridge at the time of his death. He was the Lucasian Professor of Mathematics at the University of Cambridge between 1979 and 2009.

A position representation is the parameters used to express a position relative to a reference. When representing positions relative to the Earth, it is often most convenient to represent vertical position separately, and to use some other parameters to represent horizontal position. There are also several applications where only the horizontal position is of interest, this might e.g. be the case for ships and ground vehicles/cars. It is a type of geographic coordinate system.












