
In physics, interference is a phenomenon in which two coherent waves are combined by adding their intensities or displacements with due consideration for their phase difference. The resultant wave may have greater intensity or lower amplitude if the two waves are in phase or out of phase, respectively. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves as well as in loudspeakers as electrical waves.

The Mach–Zehnder interferometer is a device used to determine the relative phase shift variations between two collimated beams derived by splitting light from a single source. The interferometer has been used, among other things, to measure phase shifts between the two beams caused by a sample or a change in length of one of the paths. The apparatus is named after the physicists Ludwig Mach and Ludwig Zehnder; Zehnder's proposal in an 1891 article was refined by Mach in an 1892 article. Mach–Zehnder interferometry with electrons as well as with light has been demonstrated. The versatility of the Mach–Zehnder configuration has led to its being used in a range of research topics efforts especially in fundamental quantum mechanics.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
Spatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler some seventy years earlier than Hamilton to solve the problem of magic squares. For this reason the dynamics community commonly refers to quaternions in this application as "Euler parameters".

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. Routhian mechanics is equivalent to Lagrangian mechanics and Hamiltonian mechanics, and introduces no new physics. It offers an alternative way to solve mechanical problems.
There are several equivalent ways for defining trigonometric functions, and the proofs of the trigonometric identities between them depend on the chosen definition. The oldest and most elementary definitions are based on the geometry of right triangles. The proofs given in this article use these definitions, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

The lateral earth pressure is the pressure that soil exerts in the horizontal direction. It is important because it affects the consolidation behavior and strength of the soil and because it is considered in the design of geotechnical engineering structures such as retaining walls, basements, tunnels, deep foundations and braced excavations.
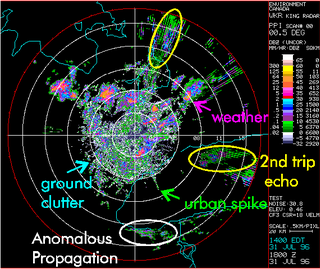
Clutter is the unwanted return (echoes) in electronic systems, particularly in reference to radars. Such echoes are typically returned from ground, sea, rain, animals/insects, chaff and atmospheric turbulences, and can cause serious performance issues with radar systems. What one person considers to be unwanted clutter, another may consider to be a wanted target. However, targets usually refer to point scatterers and clutter to extended scatterers. The clutter may fill a volume or be confined to a surface. A knowledge of the volume or surface area illuminated is required to estimated the echo per unit volume, η, or echo per unit surface area, σ°.
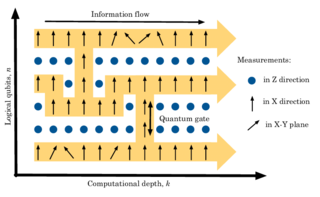
The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.

In mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow. Unlike a real fluid, this solution indicates a net zero drag on the body, a result known as d'Alembert's paradox.
Quantum mechanics was first applied to optics, and interference in particular, by Paul Dirac. Richard Feynman, in his Lectures on Physics, uses Dirac's notation to describe thought experiments on double-slit interference of electrons. Feynman's approach was extended to N-slit interferometers for either single-photon illumination, or narrow-linewidth laser illumination, that is, illumination by indistinguishable photons, by Frank Duarte. The N-slit interferometer was first applied in the generation and measurement of complex interference patterns.

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they are characterized by their phase, and therefore the algorithm can be equivalently described as retrieving either the phase or the eigenvalue itself. The algorithm was initially introduced by Alexei Kitaev in 1995.
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
In physics and engineering, Davenport chained rotations are three chained intrinsic rotations about body-fixed specific axes. Euler rotations and Tait–Bryan rotations are particular cases of the Davenport general rotation decomposition. The angles of rotation are called Davenport angles because the general problem of decomposing a rotation in a sequence of three was studied first by Paul B. Davenport.
In the field of fluid dynamics, a Rankine half body is a feature of fluid flow discovered by Scottish physicist and engineer William Rankine that is formed when a fluid source is added to a fluid undergoing potential flow. Superposition of uniform flow and source flow yields the Rankine half body flow. A practical example of this type of flow is a bridge pier or a strut placed in a uniform stream. The resulting stream function and velocity potential are obtained by simply adding the stream function and velocity potential for each individual flow.
In the larger context of the Navier-Stokes equations, elementary flows are basic flows that can be combined, using various techniques, to construct more complex flows. In this article the term "flow" is used interchangeably with the term "solution" due to historical reasons.






































