Related Research Articles

Control engineering or control systems engineering is an engineering discipline that deals with control systems, applying control theory to design equipment and systems with desired behaviors in control environments. The discipline of controls overlaps and is usually taught along with electrical engineering and mechanical engineering at many institutions around the world.
Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
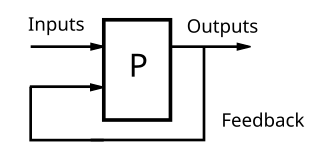
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to feed back into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems:
Simple causal reasoning about a feedback system is difficult because the first system influences the second and second system influences the first, leading to a circular argument. This makes reasoning based upon cause and effect tricky, and it is necessary to analyze the system as a whole. As provided by Webster, feedback in business is the transmission of evaluative or corrective information about an action, event, or process to the original or controlling source.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
A proportional–integral–derivative controller is a control loop mechanism employing feedback that is widely used in industrial control systems and a variety of other applications requiring continuously modulated control. A PID controller continuously calculates an error value as the difference between a desired setpoint (SP) and a measured process variable (PV) and applies a correction based on proportional, integral, and derivative terms, hence the name.

A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process.
H∞methods are used in control theory to synthesize controllers to achieve stabilization with guaranteed performance. To use H∞ methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. H∞ techniques have the advantage over classical control techniques in that H∞ techniques are readily applicable to problems involving multivariate systems with cross-coupling between channels; disadvantages of H∞ techniques include the level of mathematical understanding needed to apply them successfully and the need for a reasonably good model of the system to be controlled. It is important to keep in mind that the resulting controller is only optimal with respect to the prescribed cost function and does not necessarily represent the best controller in terms of the usual performance measures used to evaluate controllers such as settling time, energy expended, etc. Also, non-linear constraints such as saturation are generally not well-handled. These methods were introduced into control theory in the late 1970s-early 1980s by George Zames, J. William Helton , and Allen Tannenbaum.

Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
In mathematical optimization and decision theory, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite, in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy.

Richard Ernest Bellman was an American applied mathematician, who introduced dynamic programming in 1953, and made important contributions in other fields of mathematics, such as biomathematics. He founded the leading biomathematical journal Mathematical Biosciences.
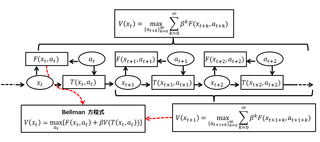
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.

In the design of experiments, optimal designs are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith.
Perceptual control theory (PCT) is a model of behavior based on the properties of negative feedback control loops. A control loop maintains a sensed variable at or near a reference value by means of the effects of its outputs upon that variable, as mediated by physical properties of the environment. In engineering control theory, reference values are set by a user outside the system. An example is a thermostat. In a living organism, reference values for controlled perceptual variables are endogenously maintained. Biological homeostasis and reflexes are simple, low-level examples. The discovery of mathematical principles of control introduced a way to model a negative feedback loop closed through the environment, which spawned perceptual control theory. It differs fundamentally from theories of behaviorism and cognitive psychology which model stimuli as causes of behavior. PCT research is published in experimental psychology, neuroscience, ethology, anthropology, linguistics, sociology, robotics, developmental psychology, organizational psychology and management, and a number of other fields. PCT has been applied to design and administration of educational systems, and has led to a psychotherapy called the method of levels.

In control theory, a bang–bang controller, is a feedback controller that switches abruptly between two states. These controllers may be realized in terms of any element that provides hysteresis. They are often used to control a plant that accepts a binary input, for example a furnace that is either completely on or completely off. Most common residential thermostats are bang–bang controllers. The Heaviside step function in its discrete form is an example of a bang–bang control signal. Due to the discontinuous control signal, systems that include bang–bang controllers are variable structure systems, and bang–bang controllers are thus variable structure controllers.
The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time period. Inspired by, but distinct from, the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian.
The value function of an optimization problem gives the value attained by the objective function at a solution, while only depending on the parameters of the problem. In a controlled dynamical system, the value function represents the optimal payoff of the system over the interval [t, t1] when started at the time-t state variable x(t)=x. If the objective function represents some cost that is to be minimized, the value function can be interpreted as the cost to finish the optimal program, and is thus referred to as "cost-to-go function." In an economic context, where the objective function usually represents utility, the value function is conceptually equivalent to the indirect utility function.
An algebraic Riccati equation is a type of nonlinear equation that arises in the context of infinite-horizon optimal control problems in continuous time or discrete time.
Stochastic control or stochastic optimal control is a sub field of control theory that deals with the existence of uncertainty either in observations or in the noise that drives the evolution of the system. The system designer assumes, in a Bayesian probability-driven fashion, that random noise with known probability distribution affects the evolution and observation of the state variables. Stochastic control aims to design the time path of the controlled variables that performs the desired control task with minimum cost, somehow defined, despite the presence of this noise. The context may be either discrete time or continuous time.
Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.
References
- ↑ Ferguson, Brian S.; Lim, G. C. (1998). Introduction to Dynamic Economic Problems. Manchester: Manchester University Press. p. 162. ISBN 0-7190-4996-2.
- ↑ Léonard, Daniel; Long, Ngo Van (1992). Optimal Control Theory and Static Optimization in Economics. New York: Cambridge University Press. p. 181. ISBN 0-521-33158-7.