
Georg Ferdinand Ludwig Philipp Cantor was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

In mathematics and formal logic, a theorem is a statement that has been proven, or can be proven. The proof of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems.

Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.
In physics, a correspondence principle is any one of several premises or assertions about the relationship between classical and quantum mechanics. The physicist Niels Bohr coined the term in 1920 during the early development of quantum theory; he used it to explain how quantized classical orbitals connect to quantum radiation. Modern sources often use the term for the idea that the behavior of systems described by quantum theory reproduces classical physics in the limit of large quantum numbers: for large orbits and for large energies, quantum calculations must agree with classical calculations. A "generalized" correspondence principle refers to the requirement for a broad set of connections between any old and new theory.
There have been several attempts in history to reach a unified theory of mathematics. Some of the most respected mathematicians in the academia have expressed views that the whole subject should be fitted into one theory.
Reciprocity may refer to:
Correspondence may refer to:
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a certain field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Marshall H. Stone. Stone was led to it by his study of the spectral theory of operators on a Hilbert space.
In mathematics, algebraic geometry and analytic geometry are two closely related subjects. While algebraic geometry studies algebraic varieties, analytic geometry deals with complex manifolds and the more general analytic spaces defined locally by the vanishing of analytic functions of several complex variables. The deep relation between these subjects has numerous applications in which algebraic techniques are applied to analytic spaces and analytic techniques to algebraic varieties.
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphism
In mathematics and mathematical physics, potential theory is the study of harmonic functions.
Continuity or continuous may refer to:
In mathematical logic, the theory of infinite sets was first developed by Georg Cantor. Although this work has become a thoroughly standard fixture of classical set theory, it has been criticized in several areas by mathematicians and philosophers.
In mathematics, comparison theorems are theorems whose statement involves comparisons between various mathematical objects of the same type, and often occur in fields such as calculus, differential equations and Riemannian geometry.

Foundations of Economic Analysis is a book by Paul A. Samuelson published in 1947 by Harvard University Press. It is based on Samuelson's 1941 doctoral dissertation at Harvard University. The book sought to demonstrate a common mathematical structure underlying multiple branches of economics from two basic principles: maximizing behavior of agents and stability of equilibrium as to economic systems. Among other contributions, it advanced the theory of index numbers and generalized welfare economics. It is especially known for definitively stating and formalizing qualitative and quantitative versions of the "comparative statics" method for calculating how a change in any parameter affects an economic system. One of its key insights about comparative statics, called the correspondence principle, states that stability of equilibrium implies testable predictions about how the equilibrium changes when parameters are changed.

Pierre de Fermat was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he is recognized for his discovery of an original method of finding the greatest and the smallest ordinates of curved lines, which is analogous to that of differential calculus, then unknown, and his research into number theory. He made notable contributions to analytic geometry, probability, and optics. He is best known for his Fermat's principle for light propagation and his Fermat's Last Theorem in number theory, which he described in a note at the margin of a copy of Diophantus' Arithmetica. He was also a lawyer at the Parlement of Toulouse, France.
Isomorphism or isomorph may refer to:
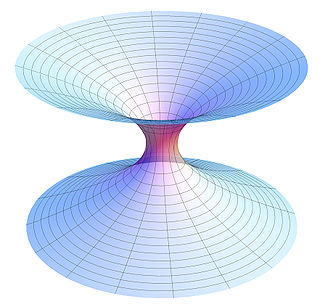
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena.
In mathematics, a reflection principle may refer to:

In mathematics, and especially algebraic geometry, stability is a notion which characterises when a geometric object, for example a point, an algebraic variety, a vector bundle, or a sheaf, has some desirable properties for the purpose of classifying them. The exact characterisation of what it means to be stable depends on the type of geometric object, but all such examples share the property of having a minimal amount of internal symmetry, that is such stable objects have few automorphisms. This is related to the concept of simplicity in mathematics, which measures when some mathematical object has few subobjects inside it. In addition to stability, some objects may be described with terms such as semi-stable, polystable, or unstable.
This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.






