Coupling (disambiguation)

Last updated October 31, 2019

Coupling is a connection or joint between two things.

Coupling construction detail used to connect two shafts (that can but do not have to be misaligned or moving or similar) together at their ends for the purpose of transmitting power

A coupling is a device used to connect two shafts together at their ends for the purpose of transmitting power. The primary purpose of couplings is to join two pieces of rotating equipment while permitting some degree of misalignment or end movement or both. In a more general context, a coupling can also be a mechanical device that serves to connect the ends of adjacent parts or objects. Couplings do not normally allow disconnection of shafts during operation, however there are torque limiting couplings which can slip or disconnect when some torque limit is exceeded. Selection, installation and maintenance of couplings can lead to reduced maintenance time and maintenance cost.

Coupling may also refer to:

Coupling (physics), when two systems are interacting with each other
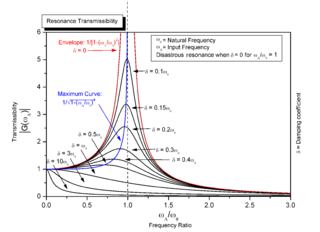
- Rotational–vibrational coupling, occurring when rotation frequency of an object is close to or identical to a natural internal vibration frequency
- Angular momentum coupling, the combining of quantized angular momentum (e.g., the interaction between two nuclei in nuclear magnetic resonance)
- Quantum coupling, when quantum states in one of the systems will cause an instantaneous change in all of the bound systems
Quantum Coupling is an effect in quantum mechanics in which two or more quantum systems are bound such that a change in one of the quantum states in one of the systems will cause an instantaneous change in all of the bound systems. It is a state similar to quantum entanglement but whereas quantum entanglement can take place over long distances quantum coupling is restricted to quantum scales.
Coupling (computer programming), the degree to which each program module relies on each one of the other modules
Coupling (electronics), the transfer of a signal from one medium or circuit block to another
Coupling (genetics), a type of genetic linkage
Coupling (piping), a short length of pipe or tube to connect two pipes or tubes together
Coupling (probability), a proof technique in probability theory
Railway coupling, a mechanism for connecting railway rolling stock
Azo coupling, often called "coupling", an electrophilic substitution reaction
Coupling reaction, reactions between hydrocarbon fragments in organic chemistry
Hose coupling, a piece on the end of a hose to connect it to extra hoses or hose appliances
Coupling track, a term in music recording for a B-side track
Joint encoding, an audio compression technique in which the redundancy of information between audio channels is reduced; also commonly known as channel coupling or stereo coupling
Mating or the act of sexual intercourse
Coupling, the distance formed by the lumbar vertebrae of a horse's back.

In physics, two objects are said to be coupled when they are interacting with each other. In classical mechanics, coupling is a connection between two oscillating systems, such as pendulums connected by a string. The connection affects the oscillatory pattern of both objects. In particle physics, two particles are coupled if they are connected by one of the four fundamental forces.

Rotational–vibrational coupling occurs when the rotation frequency of an object is close to or identical to a natural internal vibration frequency. The animation on the right shows a simple example. The motion depicted in the animation is for the idealized situation that the force exerted by the spring increases linearly with the distance to the center of rotation. Also, the animation depicts what would occur if there would not be any friction.

In quantum mechanics, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin–orbit interaction, in which case the complete physical picture must include spin-orbit coupling. Or two charged particles, each with a well-defined angular momentum, may interact by Coulomb forces, in which case coupling of the two one-particle angular momenta to a total angular momentum is a useful step in the solution of the two-particle Schrödinger equation. In both cases the separate angular momenta are no longer constants of motion, but the sum of the two angular momenta usually still is. Angular momentum coupling in atoms is of importance in atomic spectroscopy. Angular momentum coupling of electron spins is of importance in quantum chemistry. Also in the nuclear shell model angular momentum coupling is ubiquitous.

Television

Coupling (UK TV series), a British sitcom written by Steven Moffat for the BBC
- Coupling (U.S. TV series), a short-lived American sitcom based on the British series
- Coupling (Greek TV series), a short-lived Greek sitcom based on the British series

Coupling is a 2007 Greek remake of the British television sitcom of the same title which aired on ANT1.

Related Research Articles

Diatomic molecule molecule composed of only two atoms of the same or different chemical elements

Diatomic molecules are molecules composed of only two atoms, of the same or different chemical elements. The prefix di- is of Greek origin, meaning "two". If a diatomic molecule consists of two atoms of the same element, such as hydrogen (H₂) or oxygen (O₂), then it is said to be homonuclear. Otherwise, if a diatomic molecule consists of two different atoms, such as carbon monoxide (CO) or nitric oxide (NO), the molecule is said to be heteronuclear. The bond in a homonuclear diatomic molecule is non-polar.

Oscillation repetitive variation of some measure about a central value

Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. The term vibration is precisely used to describe mechanical oscillation. Familiar examples of oscillation include a swinging pendulum and alternating current.

Resonance phenomenon in which a vibrating system or external force drives another system to oscillate with greater amplitude at specific frequencies

Resonance describes the phenomena of amplification that occurs when the frequency of a periodically applied force is in harmonic proportion to a natural frequency of the system on which it acts. When an oscillating force is applied at the resonant frequency of another system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies.

Normal mode pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at the fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. When relating to music, normal modes of vibrating instruments are called "harmonics" or "overtones".

Rotational–vibrational spectroscopy is a branch of molecular spectroscopy concerned with infrared and Raman spectra of molecules in the gas phase. Transitions involving changes in both vibrational and rotational states can be abbreviated as rovibrational transitions. When such transitions emit or absorb photons, the frequency is proportional to the difference in energy levels and can be detected by certain kinds of spectroscopy. Since changes in rotational energy levels are typically much smaller than changes in vibrational energy levels, changes in rotational state are said to give fine structure to the vibrational spectrum. For a given vibrational transition, the same theoretical treatment as for pure rotational spectroscopy gives the rotational quantum numbers, energy levels, and selection rules. In linear and spherical top molecules, rotational lines are found as simple progressions at both higher and lower frequencies relative to the pure vibration frequency. In symmetric top molecules the transitions are classified as parallel when the dipole moment change is parallel to the principal axis of rotation, and perpendicular when the change is perpendicular to that axis. The ro-vibrational spectrum of the asymmetric rotor water is important because of the presence of water vapor in the atmosphere.

Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The spectra of polar molecules can be measured in absorption or emission by microwave spectroscopy or by far infrared spectroscopy. The rotational spectra of non-polar molecules cannot be observed by those methods, but can be observed and measured by Raman spectroscopy. Rotational spectroscopy is sometimes referred to as pure rotational spectroscopy to distinguish it from rotational-vibrational spectroscopy where changes in rotational energy occur together with changes in vibrational energy, and also from ro-vibronic spectroscopy where rotational, vibrational and electronic energy changes occur simultaneously.

Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that determine the position of each atom.

The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was rather a set of heuristic corrections to classical mechanics. The theory is now understood as the semi-classical approximation to modern quantum mechanics.

In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products.

The magic angle is a precisely defined angle, the value of which is approximately 54.7356°. The magic angle is a root of a second-order Legendre polynomial, P₂(cos θ) = 0, and so any interaction which depends on this second-order Legendre polynomial vanishes at the magic angle. This property makes the magic angle of particular importance in magic angle spinning solid-state NMR spectroscopy. In magnetic resonance imaging, structures with ordered collagen, such as tendons and ligaments, oriented at the magic angle may appear hyperintense in some sequences; this is called the magic angle artifact or effect.

In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of 1/2. The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of 1/2 means that the particle must be fully rotated twice before it has the same configuration as when it started.

In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry. In both classical and quantum mechanical systems, angular momentum is one of the three fundamental properties of motion.

Many first principles in quantum field theory are explained, or get further insight, in string theory.

Nuclear magnetic resonance (NMR) is a physical observation in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. Nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics, crystals as well as non-crystalline materials. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI).

In rotational-vibrational and electronic spectroscopy of diatomic molecules, Hund's coupling cases are idealized descriptions of rotational states in which specific terms in the molecular Hamiltonian and involving couplings between angular momenta are assumed to dominate over all other terms. There are five cases, proposed by Friedrich Hund in 1926-27 and traditionally denoted by the letters (a) through (e). Most diatomic molecules are somewhere between the idealized cases (a) and (b).

Orbital angular momentum (OAM) multiplexing is a physical layer method for multiplexing signals carried on electromagnetic waves using the orbital angular momentum of the electromagnetic waves to distinguish between the different orthogonal signals.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Coupling (disambiguation)

Television

See also

Related Research Articles