Electrical resistivity is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a 1 m3 solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.
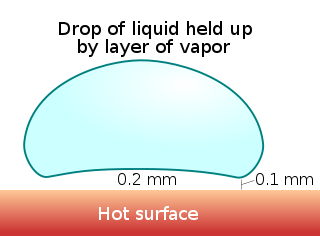
The Leidenfrost effect is a physical phenomenon in which a liquid, close to a solid surface of another body that is significantly hotter than the liquid's boiling point, produces an insulating vapor layer that keeps the liquid from boiling rapidly. Because of this repulsive force, a droplet hovers over the surface, rather than making physical contact with it. The effect is named after the German doctor Johann Gottlob Leidenfrost, who described it in A Tract About Some Qualities of Common Water.
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold. It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is flat, i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse.
In continuum mechanics, the Froude number is a dimensionless number defined as the ratio of the flow inertia to the external force field. The Froude number is based on the speed–length ratio which he defined as: where u is the local flow velocity, g is the local gravity field, and L is a characteristic length.

A capillary wave is a wave traveling along the phase boundary of a fluid, whose dynamics and phase velocity are dominated by the effects of surface tension.

In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the fetch. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over 30 m (100 ft) high, being limited by wind speed, duration, fetch, and water depth.

Animal locomotion on the surface layer of water is the study of animal locomotion in the case of small animals that live on the surface layer of water, relying on surface tension to stay afloat.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, and hydrology.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.
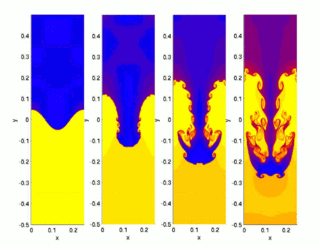
The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called (de) Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In physical oceanography, Langmuir circulation consists of a series of shallow, slow, counter-rotating vortices at the ocean's surface aligned with the wind. These circulations are developed when wind blows steadily over the sea surface. Irving Langmuir discovered this phenomenon after observing windrows of seaweed in the Sargasso Sea in 1927. Langmuir circulations circulate within the mixed layer; however, it is not yet so clear how strongly they can cause mixing at the base of the mixed layer.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
In physical oceanography, undertow is the undercurrent that moves offshore while waves approach the shore. Undertow is a natural and universal feature for almost any large body of water; it is a return flow compensating for the onshore-directed average transport of water by the waves in the zone above the wave troughs. The undertow's flow velocities are generally strongest in the surf zone, where the water is shallow and the waves are high due to shoaling.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.
Flotation of flexible objects is a phenomenon in which the bending of a flexible material allows an object to displace a greater amount of fluid than if it were completely rigid. This ability to displace more fluid translates directly into an ability to support greater loads, giving the flexible structure an advantage over a similarly rigid one. Inspiration to study the effects of elasticity are taken from nature, where plants, such as black pepper, and animals living at the water surface have evolved to take advantage of the load-bearing benefits elasticity imparts.
In physical oceanography and fluid mechanics, the Miles-Phillips mechanism describes the generation of wind waves from a flat sea surface by two distinct mechanisms. Wind blowing over the surface generates tiny wavelets. These wavelets develop over time and become ocean surface waves by absorbing the energy transferred from the wind. The Miles-Phillips mechanism is a physical interpretation of these wind-generated surface waves.
Both mechanisms are applied to gravity-capillary waves and have in common that waves are generated by a resonance phenomenon. The Miles mechanism is based on the hypothesis that waves arise as an instability of the sea-atmosphere system. The Phillips mechanism assumes that turbulent eddies in the atmospheric boundary layer induce pressure fluctuations at the sea surface. The Phillips mechanism is generally assumed to be important in the first stages of wave growth, whereas the Miles mechanism is important in later stages where the wave growth becomes exponential in time.
















