
Linear algebra is the branch of mathematics concerning linear equations such as:
In mathematics, a product is the result of multiplication, or an expression that identifies factors to be multiplied. For example, 30 is the product of 6 and 5, and is the product of and .

A vector space is a set of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. To specify that the scalars are real or complex numbers, the terms real vector space and complex vector space are often used.

In Euclidean geometry, an affine transformation, or an affinity, is a geometric transformation that preserves lines and parallelism.

In mathematics, the name symplectic group can refer to two different, but closely related, collections of mathematical groups, denoted Sp(2n, F) and Sp(n) for positive integer n and field F. The latter is called the compact symplectic group. Many authors prefer slightly different notations, usually differing by factors of 2. The notation used here is consistent with the size of the most common matrices which represent the groups. In Cartan's classification of the simple Lie algebras, the Lie algebra of the complex group Sp(2n, C) is denoted Cn, and Sp(n) is the compact real form of Sp(2n, C). Note that when we refer to the (compact) symplectic group it is implied that we are talking about the collection of (compact) symplectic groups, indexed by their dimension n.
In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It is also a fundamental tool in the field of operator algebras. It can be seen as the study of certain kinds of invariants of large matrices.
In mathematics and physics, a tensor field assigns a tensor to each point of a mathematical space. Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical sciences. As a tensor is a generalization of a scalar and a vector, a tensor field is a generalization of a scalar field or vector field that assigns, respectively, a scalar or vector to each point of space.

In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
In mathematics, the GrassmannianGr(k, V) is a space that parameterizes all k-dimensional linear subspaces of the n-dimensional vector space V. For example, the Grassmannian Gr(1, V) is the space of lines through the origin in V, so it is the same as the projective space of one dimension lower than V.
In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V. It does not use differential calculus, being based directly on abstract algebra, and in the most concrete cases just the theory of a system of linear equations.
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with reference to a sheaf of rings that codifies this geometric information.
In mathematics, the Grothendieck group construction constructs an abelian group from a commutative monoid M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
In algebraic geometry, divisors are a generalization of codimension-1 subvarieties of algebraic varieties. Two different generalizations are in common use, Cartier divisors and Weil divisors. Both are ultimately derived from the notion of divisibility in the integers and algebraic number fields.

In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion.
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations. Since around 1970, D-module theory has been built up, mainly as a response to the ideas of Mikio Sato on algebraic analysis, and expanding on the work of Sato and Joseph Bernstein on the Bernstein–Sato polynomial.
Affine geometry, broadly speaking, is the study of the geometrical properties of lines, planes, and their higher dimensional analogs, in which a notion of "parallel" is retained, but no metrical notions of distance or angle are. Affine spaces differ from linear spaces in that they do not have a distinguished choice of origin. So, in the words of Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps." Accordingly, a complex affine space, that is an affine space over the complex numbers, is like a complex vector space, but without a distinguished point to serve as the origin.
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaf cohomology is a technique for producing functions with specified properties. Many geometric questions can be formulated as questions about the existence of sections of line bundles or of more general coherent sheaves; such sections can be viewed as generalized functions. Cohomology provides computable tools for producing sections, or explaining why they do not exist. It also provides invariants to distinguish one algebraic variety from another.
Projective space plays a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of projective space.
This is a glossary of algebraic geometry.
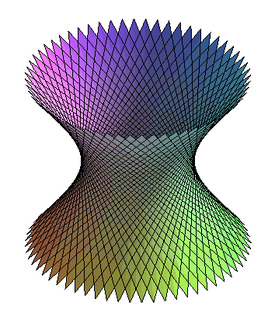
In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface

















