In physics the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force of

Coaxial cable, or coax is a type of electrical cable that has an inner conductor surrounded by a tubular insulating layer, surrounded by a tubular conducting shield. Many coaxial cables also have an insulating outer sheath or jacket. The term coaxial comes from the inner conductor and the outer shield sharing a geometric axis. Coaxial cable was invented by English engineer and mathematician Oliver Heaviside, who patented the design in 1880.

In electromagnetism, absolute permittivity, often simply called permittivity, usually denoted by the Greek letter ε (epsilon), is the measure of capacitance that is encountered when forming an electric field in a particular medium. More specifically, permittivity describes the amount of charge needed to generate one unit of electric flux in a particular medium. Accordingly, a charge will yield more electric flux in a medium with low permittivity than in a medium with high permittivity. Permittivity is the measure of a material's ability to store an electric field in the polarization of the medium.

In electromagnetism and electronics, inductance describes the tendency of an electrical conductor, such as coil, to oppose a change in the electric current through it. The change in current induces a reverse electromotive force (voltage). When an electric current flows through a conductor, it creates a magnetic field around that conductor. A changing current, in turn, creates a changing magnetic field, the surface integral of which is known as magnetic flux. From Faraday's law of induction, any change in magnetic flux through a circuit induces an electromotive force (voltage) across that circuit, a phenomenon known as electromagnetic induction. Inductance is specifically defined as the ratio between this induced voltage and the rate of change of the current in the circuit
In physics, the dissipation factor (DF) is a measure of loss-rate of energy of a mode of oscillation in a dissipative system. It is the reciprocal of quality factor, which represents the "quality" or durability of oscillation.
A magnetic circuit is made up of one or more closed loop paths containing a magnetic flux. The flux is usually generated by permanent magnets or electromagnets and confined to the path by magnetic cores consisting of ferromagnetic materials like iron, although there may be air gaps or other materials in the path. Magnetic circuits are employed to efficiently channel magnetic fields in many devices such as electric motors, generators, transformers, relays, lifting electromagnets, SQUIDs, galvanometers, and magnetic recording heads.
Permeance, in general, is the degree to which a material admits a flow of matter or energy. Permeance is usually represented by a curly capital P: .
Magnetic complex reluctance is a measurement of a passive magnetic circuit dependent on sinusoidal magnetomotive force and sinusoidal magnetic flux, and this is determined by deriving the ratio of their complex effective amplitudes.[Ref. 1-3]

The Maxwell stress tensor is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impossibly difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
The method of image charges is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.

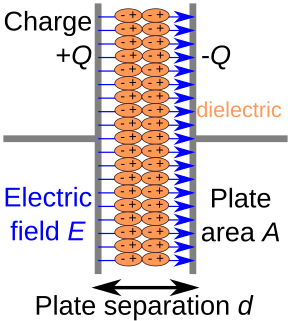
A capacitor is a passive two-terminal electronic component that stores electrical energy in an electric field. The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit. The capacitor was originally known as a condenser or condensator. The original name is still widely used in many languages, but not commonly in English.
Dielectric loss quantifies a dielectric material's inherent dissipation of electromagnetic energy. It can be parameterized in terms of either the loss angleδ or the corresponding loss tangent tan δ. Both refer to the phasor in the complex plane whose real and imaginary parts are the resistive (lossy) component of an electromagnetic field and its reactive (lossless) counterpart.

A microwave cavity or radio frequency (RF) cavity is a special type of resonator, consisting of a closed metal structure that confines electromagnetic fields in the microwave region of the spectrum. The structure is either hollow or filled with dielectric material. The microwaves bounce back and forth between the walls of the cavity. At the cavity's resonant frequencies they reinforce to form standing waves in the cavity. Therefore, the cavity functions similarly to an organ pipe or sound box in a musical instrument, oscillating preferentially at a series of frequencies, its resonant frequencies. Thus it can act as a bandpass filter, allowing microwaves of a particular frequency to pass while blocking microwaves at nearby frequencies.
The gyrator–capacitor model is a lumped-element model for magnetic fields, similar to magnetic circuits, but based on using elements analogous to capacitors rather than elements analogous to resistors to represent the magnetic flux path. Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:

Surface plasmon polaritons (SPPs) are infrared or visible-frequency electromagnetic waves that travel along a metal–dielectric or metal–air interface. The term "surface plasmon polariton" explains that the wave involves both charge motion in the metal and electromagnetic waves in the air or dielectric ("polariton").
Cavity perturbation theory describes methods for derivation of perturbation formulae for performance changes of a cavity resonator. These performance changes are assumed to be caused by either introduction of a small foreign object into the cavity or a small deformation of its boundary.
In condensed matter physics and physical chemistry, the Lifshitz theory of van der Waals forces, sometimes called the macroscopic theory of van der Waals forces, is a method proposed by Evgeny Mikhailovich Lifshitz in 1954 for treating van der Waals forces between bodies which does not assume pairwise additivity of the individual intermolecular forces; that is to say, the theory takes into account the influence of neighboring molecules on the interaction between every pair of molecules located in the two bodies, rather than treating each pair independently.