
Molecular diffusion, often simply called diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a phase with uniform temperature, absent external net forces acting on the particles, the diffusion process will eventually result in complete mixing.

Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.
Mass transfer is the net movement of mass from one location to another. Mass transfer occurs in many processes, such as absorption, evaporation, drying, precipitation, membrane filtration, and distillation. Mass transfer is used by different scientific disciplines for different processes and mechanisms. The phrase is commonly used in engineering for physical processes that involve diffusive and convective transport of chemical species within physical systems.
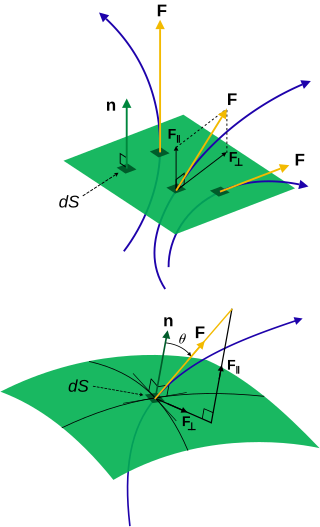
Flux describes any effect that appears to pass or travel through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface.
A dimensionless quantity is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one, which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time. Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians.
In continuum mechanics, the Péclet number is a class of dimensionless numbers relevant in the study of transport phenomena in a continuum. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient. In the context of species or mass transfer, the Péclet number is the product of the Reynolds number and the Schmidt number. In the context of the thermal fluids, the thermal Péclet number is equivalent to the product of the Reynolds number and the Prandtl number.
Graham's law of effusion was formulated by Scottish physical chemist Thomas Graham in 1848. Graham found experimentally that the rate of effusion of a gas is inversely proportional to the square root of the molar mass of its particles. This formula is stated as:
The Sherwood number (Sh) is a dimensionless number used in mass-transfer operation. It represents the ratio of the convective mass transfer to the rate of diffusive mass transport, and is named in honor of Thomas Kilgore Sherwood.
Diffusion is a time-dependent random process causing a spread in space.

Gaseous diffusion is a technology used to produce enriched uranium by forcing gaseous uranium hexafluoride (UF6) through semipermeable membranes. This produces a slight separation between the molecules containing uranium-235 (235U) and uranium-238 (238U). By use of a large cascade of many stages, high separations can be achieved. It was the first process to be developed that was capable of producing enriched uranium in industrially useful quantities, but is nowadays considered obsolete, having been superseded by the more-efficient gas centrifuge process.
Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).
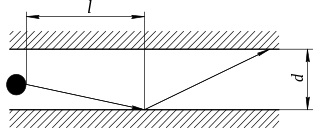
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore with a narrow diameter (2–50 nm) because molecules frequently collide with the pore wall.

Eddy diffusion, eddy dispersion, or turbulent diffusion is a process by which substances are mixed in the atmosphere, the ocean or in any fluid system due to eddy motion. In other words, it is mixing that is caused by eddies that can vary in size from subtropical ocean gyres down to the small Kolmogorov microscales. The concept of turbulence or turbulent flow causes eddy diffusion to occur. The theory of eddy diffusion was first developed by Sir Geoffrey Ingram Taylor.
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry.

Surface diffusion is a general process involving the motion of adatoms, molecules, and atomic clusters (adparticles) at solid material surfaces. The process can generally be thought of in terms of particles jumping between adjacent adsorption sites on a surface, as in figure 1. Just as in bulk diffusion, this motion is typically a thermally promoted process with rates increasing with increasing temperature. Many systems display diffusion behavior that deviates from the conventional model of nearest-neighbor jumps. Tunneling diffusion is a particularly interesting example of an unconventional mechanism wherein hydrogen has been shown to diffuse on clean metal surfaces via the quantum tunneling effect.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models has applications in several fields, beyond physics, such as statistics, probability theory, information theory, neural networks, finance and marketing etc.
Turbulent diffusion is the transport of mass, heat, or momentum within a system due to random and chaotic time dependent motions. It occurs when turbulent fluid systems reach critical conditions in response to shear flow, which results from a combination of steep concentration gradients, density gradients, and high velocities. It occurs much more rapidly than molecular diffusion and is therefore extremely important for problems concerning mixing and transport in systems dealing with combustion, contaminants, dissolved oxygen, and solutions in industry. In these fields, turbulent diffusion acts as an excellent process for quickly reducing the concentrations of a species in a fluid or environment, in cases where this is needed for rapid mixing during processing, or rapid pollutant or contaminant reduction for safety.

Double diffusive convection is a fluid dynamics phenomenon that describes a form of convection driven by two different density gradients, which have different rates of diffusion.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
Equimolar counterdiffusion is an instance of molecular diffusion in a binary mixture, and occurs when equal numbers of molecules of the two substances are moving in opposite directions.







