Thermal conduction is the transfer of heat internal energy by microscopic collisions of particles and movement of electrons within a body. The microscopically colliding particles, that include molecules, atoms and electrons, transfer disorganized microscopic kinetic and potential energy, jointly known as internal energy. Conduction takes place in all phases of solids, liquids, gases and waves. The rate at which energy is conducted as heat between two bodies is a function of the temperature difference temperature gradient between the two bodies and the properties of the conductive interface through which the heat is transferred.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as engineering geology, geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.
Used in hydrogeology, the groundwater flow equation is the mathematical relationship which is used to describe the flow of groundwater through an aquifer. The transient flow of groundwater is described by a form of the diffusion equation, similar to that used in heat transfer to describe the flow of heat in a solid. The steady-state flow of groundwater is described by a form of the Laplace equation, which is a form of potential flow and has analogs in numerous fields.

Infiltration is the process by which water on the ground surface enters the soil. It is commonly used in both hydrology and soil sciences. The infiltration capacity is defined as the maximum rate of infiltration. It is most often measured in meters per day but can also be measured in other units of distance over time if necessary. The infiltration capacity decreases as the soil moisture content of soils surface layers increases. If the precipitation rate exceeds the infiltration rate, runoff will usually occur unless there is some physical barrier.
John Robert Philip AO FAA FRS was an Australian soil physicist and hydrologist, internationally recognised for his contributions to the understanding of movement of water, energy and gases. While he never performed his own experimental work, he was recognised for his skills in mathematics that could be used to explain physical processes and solve real world problems.
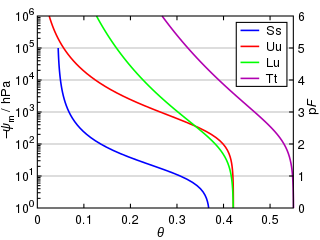
Water retention curve is the relationship between the water content, θ, and the soil water potential, ψ. This curve is characteristic for different types of soil, and is also called the soil moisture characteristic.
The United States Environmental Protection Agency (EPA) Storm Water Management Model is a dynamic rainfall–runoff–subsurface runoff simulation model used for single-event to long-term (continuous) simulation of the surface/subsurface hydrology quantity and quality from primarily urban/suburban areas. It can simulate the Rainfall- runoff, runoff, evaporation, infiltration and groundwater connection for roots, streets, grassed areas, rain gardens and ditches and pipes, for example. The hydrology component of SWMM operates on a collection of subcatchment areas divided into impervious and pervious areas with and without depression storage to predict runoff and pollutant loads from precipitation, evaporation and infiltration losses from each of the subcatchment. Besides, low impact development (LID) and best management practice areas on the subcatchment can be modeled to reduce the impervious and pervious runoff. The routing or hydraulics section of SWMM transports this water and possible associated water quality constituents through a system of closed pipes, open channels, storage/treatment devices, ponds, storages, pumps, orifices, weirs, outlets, outfalls and other regulators. SWMM tracks the quantity and quality of the flow generated within each subcatchment, and the flow rate, flow depth, and quality of water in each pipe and channel during a simulation period composed of multiple fixed or variable time steps. The water quality constituents such as water quality constituents can be simulated from buildup on the subcatchments through washoff to a hydraulic network with optional first order decay and linked pollutant removal, best management practice and low-impact development removal and treatment can be simulated at selected storage nodes. SWMM is one of the hydrology transport models which the EPA and other agencies have applied widely throughout North America and through consultants and universities throughout the world. The latest update notes and new features can be found on the EPA website in the download section. Recently added in November 2015 were the EPA SWMM 5.1 Hydrology Manual and in 2016 the EPA SWMM 5.1 Hydraulic Manual and EPA SWMM 5.1 Water Quality Volume (III) + Errata”
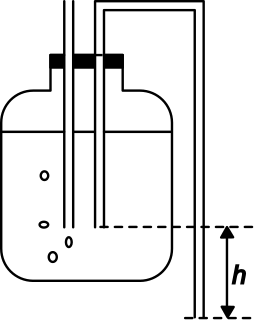
Mariotte’s bottle is a device that delivers a constant rate of flow from closed bottles or tanks. It is named after French physicist Edme Mariotte (1620-1684). A picture of a bottle with a gas inlet is shown in the works of Mariotte, but this construction was made to show the effect of outside pressure on mercury level inside the bottle. It further misses a siphon or an outlet for the liquid.
In 1957 John Philip introduced the term sorptivity and defined it as a measure of the capacity of the medium to absorb or desorb liquid by capillarity.
The Richards equation represents the movement of water in unsaturated soils, and is attributed to Lorenzo A. Richards who published the equation in 1931. It is a nonlinear partial differential equation, which is often difficult to approximate since it does not have a closed-form analytical solution. Although attributed to Richards, it is established that this equation was actually discovered 9 years earlier Lorenzo A. Richards by Lewis Fry Richardson in his book "Weather prediction by numerical process" published in 1922 (p.108).
The pore space of soil contains the liquid and gas phases of soil, i.e., everything but the solid phase that contains mainly minerals of varying sizes as well as organic compounds.
Well drainage means drainage of agricultural lands by wells. Agricultural land is drained by pumped wells to improve the soils by controlling water table levels and soil salinity.
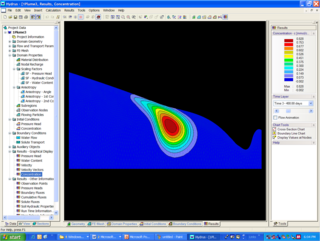
Hydrus is a suite of Windows-based modeling software that can be used for analysis of water flow, heat and solute transport in variably saturated porous media. HYDRUS suite of software is supported by an interactive graphics-based interface for data-preprocessing, discretization of the soil profile, and graphic presentation of the results. While HYDRUS-1D simulates water flow, solute and heat transport in one-dimension, and is a public domain software, HYDRUS 2D/3D extends the simulation capabilities to the second and third dimensions, and is distributed commercially.
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure the "accessible void", the total amount of void space accessible from the surface. There are many ways to test porosity in a substance or part, such as industrial CT scanning. The term porosity is used in multiple fields including pharmaceutics, ceramics, metallurgy, materials, manufacturing, hydrology, earth sciences, soil mechanics and engineering.
The following outline is provided as an overview of and topical guide to hydrology:

A drainage equation is an equation describing the relation between depth and spacing of parallel subsurface drains, depth of the watertable, depth and hydraulic conductivity of the soils. It is used in drainage design.

The finite water-content vadose zone flux method represents a one-dimensional alternative to the numerical solution of Richards' equation for simulating the movement of water in unsaturated soils. The finite water-content method is an ordinary differential equation alternative to the Richards partial differential equation. The Richards equation is difficult to approximate in general because it does not have a closed-form analytical solution except in a few cases. The finite water-content method, is perhaps the first generic replacement for the numerical solution of the Richards' equation. The finite water-content solution has several advantages over the Richards equation solution. First, as an ordinary differential equation it is explicit, guaranteed to converge and computationally inexpensive to solve. Second, using a finite volume solution methodology it is guaranteed to conserve mass. The finite water content method readily simulates sharp wetting fronts, something that the Richards solution struggles with. The main limiting assumption required to use the finite water-content method is that the soil be homogeneous in layers.
Bioclogging or biological clogging is clogging of pore space in soil by microbial biomass; their body and their byproducts such as extracellular polymeric substance (EPS). The microbial biomass blocks the pathway of water in the pore space, forming a certain thickness of impermeable layer in soil, and it reduces the rate of infiltration of water remarkably.













