 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages) (Learn how and when to remove this template message)
|
ECLR-attributed grammars are a special type of attribute grammars.
They are a variant of LR-attributed grammars where an equivalence relation on inherited attributes is used to optimize attribute evaluation. EC stands for equivalence class. Rie is based on ECLR-attributed grammars.
In computer science, an LALR parser or Look-Ahead LR parser is a simplified version of a canonical LR parser, to parse a text according to a set of production rules specified by a formal grammar for a computer language.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.
In statistics, the likelihood-ratio test assesses the goodness of fit of two competing statistical models based on the ratio of their likelihoods, specifically one found by maximization over the entire parameter space and another found after imposing some constraint. If the constraint is supported by the observed data, the two likelihoods should not differ by more than sampling error. Thus the likelihood-ratio test tests whether this ratio is significantly different from one, or equivalently whether its natural logarithm is significantly different from zero.
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding quotient structure, whose elements are the equivalence classes for the relation.
In computer science, a Simple LR or SLR parser is a type of LR parser with small parse tables and a relatively simple parser generator algorithm. As with other types of LR(1) parser, an SLR parser is quite efficient at finding the single correct bottom-up parse in a single left-to-right scan over the input stream, without guesswork or backtracking. The parser is mechanically generated from a formal grammar for the language.
In computer science, a canonical LR parser or LR(1) parser is an LR(k) parser for k=1, i.e. with a single lookahead terminal. The special attribute of this parser is that any LR(k) grammar with k>1 can be transformed into an LR(1) grammar. However, back-substitutions are required to reduce k and as back-substitutions increase, the grammar can quickly become large, repetitive and hard to understand. LR(k) can handle all deterministic context-free languages. In the past this LR(k) parser has been avoided because of its huge memory requirements in favor of less powerful alternatives such as the LALR and the LL(1) parser. Recently, however, a "minimal LR(1) parser" whose space requirements are close to LALR parsers, is being offered by several parser generators.
Parsing, syntax analysis, or syntactic analysis is the process of analyzing a string of symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar. The term parsing comes from Latin pars (orationis), meaning part.
In programming language theory, semantics is the field concerned with the rigorous mathematical study of the meaning of programming languages. It does so by evaluating the meaning of syntactically valid strings defined by a specific programming language, showing the computation involved. In such a case that the evaluation would be of syntactically invalid strings, the result would be non-computation. Semantics describes the processes a computer follows when executing a program in that specific language. This can be shown by describing the relationship between the input and output of a program, or an explanation of how the program will be executed on a certain platform, hence creating a model of computation.
An attribute grammar is a formal way to define attributes for the productions of a formal grammar, associating these attributes with values. The evaluation occurs in the nodes of the abstract syntax tree, when the language is processed by some parser or compiler.
Tree-adjoining grammar (TAG) is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol. Whereas context-free grammars have rules for rewriting symbols as strings of other symbols, tree-adjoining grammars have rules for rewriting the nodes of trees as other trees.
In computer science, a Van Wijngaarden grammar is a two-level grammar which provides a technique to define potentially infinite context-free grammars in a finite number of rules. The formalism was invented by Adriaan van Wijngaarden to define rigorously some syntactic restrictions which previously had to be formulated in natural language, despite their essentially syntactical content.
In computer science, a rough set, first described by Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set. In the standard version of rough set theory, the lower- and upper-approximation sets are crisp sets, but in other variations, the approximating sets may be fuzzy sets.
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms ('arrows') called 'weak equivalences', 'fibrations' and 'cofibrations' satisfying certain axioms relating them. These abstract from the category of topological spaces or of chain complexes. The concept was introduced by Daniel G. Quillen (1967).
Conjunctive grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with a conjunction operation. Besides explicit conjunction, conjunctive grammars allow implicit disjunction represented by multiple rules for a single nonterminal symbol, which is the only logical connective expressible in context-free grammars. Conjunction can be used, in particular, to specify intersection of languages. A further extension of conjunctive grammars known as Boolean grammars additionally allows explicit negation.
LR-attributed grammars are a special type of attribute grammars. They allow the attributes to be evaluated on LR parsing. As a result, attribute evaluation in LR-attributed grammars can be incorporated conveniently in bottom-up parsing. zyacc is based on LR-attributed grammars. They are a subset of the L-attributed grammars, where the attributes can be evaluated in one left-to-right traversal of the abstract syntax tree. They are a superset of the S-attributed grammars, which allow only synthesized attributes. In yacc, a common hack is to use global variables to simulate some kind of inherited attributes and thus LR-attribution.
In formal grammar theory, the deterministic context-free grammars (DCFGs) are a proper subset of the context-free grammars. They are the subset of context-free grammars that can be derived from deterministic pushdown automata, and they generate the deterministic context-free languages. DCFGs are always unambiguous, and are an important subclass of unambiguous CFGs; there are non-deterministic unambiguous CFGs, however.
Late Middle Japanese was a stage of the Japanese language following Early Middle Japanese and preceding Early Modern Japanese. It was a period of transition in which the language shed many of its archaic features and became closer to its modern form.
Early Modern Japanese was the stage of the Japanese language after Middle Japanese and before Modern Japanese. It is a period of transition that shed many of the language's medieval characteristics and became closer to its modern form.
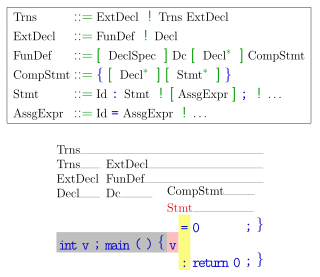
In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.
