Echo removal

Last updated

Echo removal is the process of removing echo and reverberation artifacts from audio signals. The reverberation is typically modeled as the convolution of a (sometimes time-varying) impulse response with a hypothetical clean input signal, where both the clean input signal (which is to be recovered) and the impulse response are unknown. This is an example of an inverse problem. In almost all cases, there is insufficient information in the input signal to uniquely determine a plausible original image, making it an ill-posed problem. This is generally solved by the use of a regularization term to attempt to eliminate implausible solutions.

In audio signal processing and acoustics, echo is a reflection of sound that arrives at the listener with a delay after the direct sound. The delay is directly proportional to the distance of the reflecting surface from the source and the listener. Typical examples are the echo produced by the bottom of a well, by a building, or by the walls of an enclosed room and an empty room. A true echo is a single reflection of the sound source.

Reverberation, in psychoacoustics and acoustics, is a persistence of sound after the sound is produced. A reverberation, or reverb, is created when a sound or signal is reflected causing a large number of reflections to build up and then decay as the sound is absorbed by the surfaces of objects in the space – which could include furniture, people, and air. This is most noticeable when the sound source stops but the reflections continue, decreasing in amplitude, until they reach zero amplitude.

Convolution mathematical operation

In mathematics convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. Convolution is similar to cross-correlation. For real-valued functions, of a continuous or discrete variable, it differs from cross-correlation only in that either f (x) or g(x) is reflected about the y-axis; thus it is a cross-correlation of f (x) and g(−x), or f (−x) and g(x). For continuous functions, the cross-correlation operator is the adjoint of the convolution operator.

This problem is analogous to deblurring in the image processing domain.

Deblurring is the process of removing blurring artifacts from images, such as blur caused by defocus aberration or motion blur. The blur is typically modeled as the convolution of a point spread function with a hypothetical sharp input image, where both the sharp input image and the point spread function are unknown. This is an example of an inverse problem. In almost all cases, there is insufficient information in the blurred image to uniquely determine a plausible original image, making it an ill-posed problem. In addition the blurred image contains additional noise which complicates the task of determining the original image. This is generally solved by the use of a regularization term to attempt to eliminate implausible solutions. This problem is analogous to echo removal in the signal processing domain. Nevertheless, when coherent beam is used for imaging, the point spread function can be modeled mathematically. As the figure on the right illustrates, by proper deconvolution of the point spread function and the image, the resolution can be enhanced several times.

See also

Echo suppression and echo cancellation are methods used in telephony to improve voice quality by preventing echo from being created or removing it after it is already present. In addition to improving subjective audio quality, echo suppression increases the capacity achieved through silence suppression by preventing echo from traveling across a network. Echo suppressors were developed in the 1950s in response to the first use of satellites for telecommunications, but they have since been largely supplanted by better performing echo cancellers.

Digital room correction

Digital room correction is a process in the field of acoustics where digital filters designed to ameliorate unfavorable effects of a room's acoustics are applied to the input of a sound reproduction system. Modern room correction systems produce substantial improvements in the time domain and frequency domain response of the sound reproduction system.

Noise reduction is the process of removing noise from a signal.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Related Research Articles

Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency.

Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. This results from systems composed solely of components classified as having a linear response. Most filters implemented in analog electronics, in digital signal processing, or in mechanical systems are classified as causal, time invariant, and linear signal processing filters.

Signal processing models and analyzes data representations of physical events

Signal processing is a subfield of mathematics, information and electrical engineering that concerns the analysis, synthesis, and modification of signals, which are broadly defined as functions conveying "information about the behavior or attributes of some phenomenon", such as sound, images, and biological measurements. For example, signal processing techniques are used to improve signal transmission fidelity, storage efficiency, and subjective quality, and to emphasize or detect components of interest in a measured signal.

Digital filter mechanism to reduce or enhance aspects of a sampled, discrete-time signal

In signal processing, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is an electronic circuit operating on continuous-time analog signals.

Filter design is the process of designing a signal processing filter that satisfies a set of requirements, some of which are contradictory. The purpose is to find a realization of the filter that meets each of the requirements to a sufficient degree to make it useful.

Echo chamber hollow enclosure used to produce reverberated sounds

An echo chamber is a hollow enclosure used to produce reverberation, usually for recording purposes. For example, the producers of a television or radio program might wish to produce the aural illusion that a conversation is taking place in a large room or a cave; these effects can be accomplished by playing the recording of the conversation inside an echo chamber, with an accompanying microphone to catch the reverberation. Nowadays effects units are more widely used to create such effects, but echo chambers are still used today, such as the famous echo chambers at Capitol Studios.

Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input. In simplest terms, if a sine wave is injected into a system at a given frequency, a linear system will respond at that same frequency with a certain magnitude and a certain phase angle relative to the input. Also for a linear system, doubling the amplitude of the input will double the amplitude of the output. In addition, if the system is time-invariant, then the frequency response also will not vary with time. Thus for LTI systems, the frequency response can be seen as applying the system's transfer function to a purely imaginary number argument representing the frequency of the sinusoidal excitation.

Analog signal processing is a type of signal processing conducted on continuous analog signals by some analog means. "Analog" indicates something that is mathematically represented as a set of continuous values. This differs from "digital" which uses a series of discrete quantities to represent signal. Analog values are typically represented as a voltage, electric current, or electric charge around components in the electronic devices. An error or noise affecting such physical quantities will result in a corresponding error in the signals represented by such physical quantities.

In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.

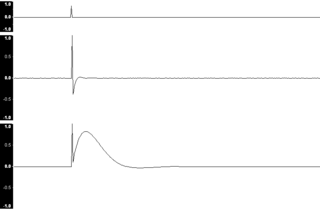
Impulse response

In signal processing, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time.

Linear time-invariant theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant system to an arbitrary input signal. Trajectories of these systems are commonly measured and tracked as they move through time, but in applications like image processing and field theory, the LTI systems also have trajectories in spatial dimensions. Thus, these systems are also called linear translation-ivariant to give the theory the most general reach. In the case of generic discrete-time systems, linear shift-invariant is the corresponding term. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors.

In a mixed-signal system, a reconstruction filter is used to construct a smooth analog signal from a digital input, as in the case of a digital to analog converter (DAC) or other sampled data output device.

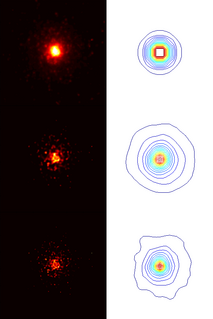
Blind deconvolution

In electrical engineering and applied mathematics, blind deconvolution is deconvolution without explicit knowledge of the impulse response function used in the convolution. This is usually achieved by making appropriate assumptions of the input to estimate the impulse response by analyzing the output. Blind deconvolution is not solvable without making assumptions on input and impulse response. Most of the algorithms to solve this problem are based on assumption that both input and impulse response live in respective known subspaces. However, blind deconvolution remains a very challenging non-convex optimization problem even with this assumption.

In audio signal processing, convolution reverb is a process used for digitally simulating the reverberation of a physical or virtual space through the use of software profiles; a piece of software that creates a simulation of an audio environment. It is based on the mathematical convolution operation, and uses a pre-recorded audio sample of the impulse response of the space being modeled. To apply the reverberation effect, the impulse-response recording is first stored in a digital signal-processing system. This is then convolved with the incoming audio signal to be processed. The process of convolution multiplies each sample of the audio to be processed (reverberated) with the samples in the impulse response file.

Ringing artifacts

In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a bell after being struck. As with other artifacts, their minimization is a criterion in filter design.

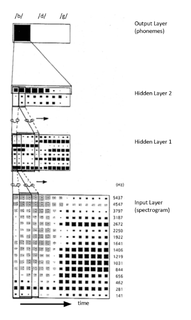
Time delay neural network

Time delay neural network (TDNN) is a multilayer artificial neural network architecture whose purpose is to 1) classify patterns with shift-invariance, and 2) model context at each layer of the network.

3D sound reconstruction is the application of reconstruction techniques to 3D sound localization technology. These methods of reconstructing three-dimensional sound are used to recreate sounds to match natural environments and provide spatial cues of the sound source. They also see applications in creating 3D visualizations on a sound field to include physical aspects of sound waves including direction, pressure, and intensity. This technology is used in entertainment to reproduce a live performance through computer speakers. The technology is also used in military applications to determine location of sound sources. Reconstructing sound fields is also applicable to medical imaging to measure points in ultrasound.

3D sound refers to the way humans experience sound in their everyday lives. In real life, people are always surrounded by sound. Sounds arrive at our ears from every direction and from varying distances. These and other factors contribute to the three-dimensional aural image humans hear. Scientists and engineers who work with 3D sound work to accurately synthesize the complexity of real-world sounds.

Transfer function filter utilizes the transfer function and the Convolution theorem to produce a filter. In this article, an example of such a filter using finite impulse response is discussed and an application of the filter into real world data is shown.