Embedding problem

Last updated

In Galois theory, a branch of mathematics, the embedding problem is a generalization of the inverse Galois problem. Roughly speaking, it asks whether a given Galois extension can be embedded into a Galois extension in such a way that the restriction map between the corresponding Galois groups is given.

Contents

Definition

Given a field K and a finite group H, one may pose the following question (the so called inverse Galois problem). Is there a Galois extension F/K with Galois group isomorphic to H. The embedding problem is a generalization of this problem:

Let L/K be a Galois extension with Galois group G and let f : H → G be an epimorphism. Is there a Galois extension F/K with Galois group H and an embedding α : L → F fixing K under which the restriction map from the Galois group of F/K to the Galois group of L/K coincides with f?

Analogously, an embedding problem for a profinite group F consists of the following data: Two profinite groups H and G and two continuous epimorphisms φ : F → G and f : H → G. The embedding problem is said to be finite if the group H is. A solution (sometimes also called weak solution) of such an embedding problem is a continuous homomorphism γ : F → H such that φ = f γ. If the solution is surjective, it is called a proper solution.

Properties

Finite embedding problems characterize profinite groups. The following theorem gives an illustration for this principle.

Theorem. Let F be a countably (topologically) generated profinite group. Then

  1. F is projective if and only if any finite embedding problem for F is solvable.
  2. F is free of countable rank if and only if any finite embedding problem for F is properly solvable.

Related Research Articles

<span class="mw-page-title-main">Field (mathematics)</span> Algebraic structure with addition, multiplication, and division

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.

In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.

In mathematics, a profinite group is a topological group that is in a certain sense assembled from a system of finite groups.

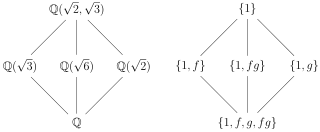
<span class="mw-page-title-main">Galois theory</span> Mathematical connection between field theory and group theory

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.

In mathematics, class field theory (CFT) is the fundamental branch of algebraic number theory whose goal is to describe all the abelian Galois extensions of local and global fields using objects associated to the ground field.

Field theory is the branch of mathematics in which fields are studied. This is a glossary of some terms of the subject.

In mathematics, Grothendieck's Galois theory is an abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry. It provides, in the classical setting of field theory, an alternative perspective to that of Emil Artin based on linear algebra, which became standard from about the 1930s.

In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa (1959), as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur considered generalizations of Iwasawa theory to abelian varieties. More recently, Ralph Greenberg has proposed an Iwasawa theory for motives.

In mathematics, a Galois module is a G-module, with G being the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring in representation theory, but can also be used as a synonym for G-module. The study of Galois modules for extensions of local or global fields and their group cohomology is an important tool in number theory.

In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.

In Galois theory, the inverse Galois problem concerns whether or not every finite group appears as the Galois group of some Galois extension of the rational numbers . This problem, first posed in the early 19th century, is unsolved.

In abstract algebra, Hilbert's Theorem 90 (or Satz 90) is an important result on cyclic extensions of fields (or to one of its generalizations) that leads to Kummer theory. In its most basic form, it states that if L/K is an extension of fields with cyclic Galois group G = Gal(L/K) generated by an element and if is an element of L of relative norm 1, that is

In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions in relation to groups. It was proved by Évariste Galois in his development of Galois theory.

<span class="mw-page-title-main">Absolute Galois group</span>

In mathematics, the absolute Galois groupGK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is well-defined up to inner automorphism. It is a profinite group.

In mathematics, a field is pseudo algebraically closed if it satisfies certain properties which hold for algebraically closed fields. The concept was introduced by James Ax in 1967.

In mathematics, in the realm of group theory, a countable group is said to be SQ-universal if every countable group can be embedded in one of its quotient groups. SQ-universality can be thought of as a measure of largeness or complexity of a group.

In mathematics, a class formation is a topological group acting on a module satisfying certain conditions. Class formations were introduced by Emil Artin and John Tate to organize the various Galois groups and modules that appear in class field theory.

In mathematics, field arithmetic is a subject that studies the interrelations between arithmetic properties of a field and its absolute Galois group. It is an interdisciplinary subject as it uses tools from algebraic number theory, arithmetic geometry, algebraic geometry, model theory, the theory of finite groups and of profinite groups.

In mathematics, an approximately finite-dimensional (AF) C*-algebra is a C*-algebra that is the inductive limit of a sequence of finite-dimensional C*-algebras. Approximate finite-dimensionality was first defined and described combinatorially by Ola Bratteli. Later, George A. Elliott gave a complete classification of AF algebras using the K0 functor whose range consists of ordered abelian groups with sufficiently nice order structure.

In mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.