
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
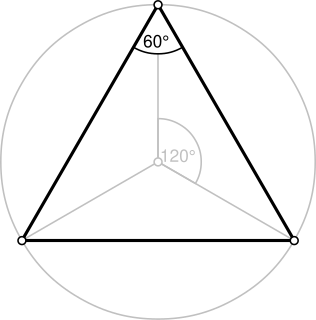
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

A right triangle or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle, is a triangle in which one angle is a right angle or two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigonometry.

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half an angle is the stereographic projection of the circle onto a line. Among these formulas are the following:

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.
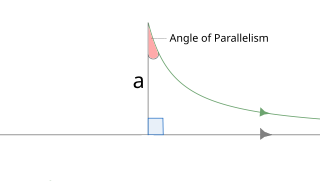
In hyperbolic geometry, the angle of parallelism , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
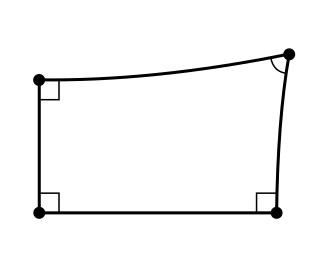
In geometry, a Lambert quadrilateral, named after Johann Heinrich Lambert, is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel postulate could be proved as a theorem. It is now known that the type of the fourth angle depends upon the geometry in which the quadrilateral exists. In hyperbolic geometry the fourth angle is acute, in Euclidean geometry it is a right angle and in elliptic geometry it is an obtuse angle.
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates.

In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted simply as and .

In relativity, proper velocityw of an object relative to an observer is the ratio between observer-measured displacement vector and proper time τ elapsed on the clocks of the traveling object:

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states
In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativistic velocity addition formula.

In mathematics, the Pythagorean theorem, or Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the legs a, b and the hypotenuse c, often called the Pythagorean equation:

There are many ways to derive the Lorentz transformations utilizing a variety of physical principles, ranging from Maxwell's equations to Einstein's postulates of special relativity, and mathematical tools, spanning from elementary algebra and hyperbolic functions, to linear algebra and group theory.
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.

In geometry, a mixtilinear incircle of a triangle is a circle tangent to two of its sides and internally tangent to its circumcircle. The mixtilinear incircle of a triangle tangent to the two sides containing vertex is called the -mixtilinear incircle. Every triangle has three unique mixtilinear incircles, one corresponding to each vertex.




































