The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.

In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio.
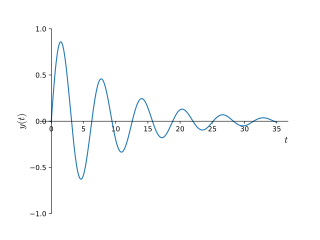
In physics and engineering, the quality factor or Q factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher Q indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high Q, while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer.
In finance, the binomial options pricing model (BOPM) provides a generalizable numerical method for the valuation of options. Essentially, the model uses a "discrete-time" model of the varying price over time of the underlying financial instrument, addressing cases where the closed-form Black–Scholes formula is wanting.
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
Rational pricing is the assumption in financial economics that asset prices - and hence asset pricing models - will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away". This assumption is useful in pricing fixed income securities, particularly bonds, and is fundamental to the pricing of derivative instruments.
In finance, arbitrage pricing theory (APT) is a multi-factor model for asset pricing which relates various macro-economic (systematic) risk variables to the pricing of financial assets. Proposed by economist Stephen Ross in 1976, it is widely believed to be an improved alternative to its predecessor, the Capital Asset Pricing Model (CAPM). APT is founded upon the law of one price, which suggests that within an equilibrium market, rational investors will implement arbitrage such that the equilibrium price is eventually realised. As such, APT argues that when opportunities for arbitrage are exhausted in a given period, then the expected return of an asset is a linear function of various factors or theoretical market indices, where sensitivities of each factor is represented by a factor-specific beta coefficient or factor loading. Consequently, it provides traders with an indication of ‘true’ asset value and enables exploitation of market discrepancies via arbitrage. The linear factor model structure of the APT is used as the basis for evaluating asset allocation, the performance of managed funds as well as the calculation of cost of capital.

In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received. When the price of an asset is considered as a function of yield, duration also measures the price sensitivity to yield, the rate of change of price with respect to yield, or the percentage change in price for a parallel shift in yields.

In probability theory, the Kelly criterion, is a formula that determines the optimal theoretical size for a bet. It is valid when the expected returns are known. The Kelly bet size is found by maximizing the expected value of the logarithm of wealth, which is equivalent to maximizing the expected geometric growth rate. J. L. Kelly Jr, a researcher at Bell Labs, described the criterion in 1956. Because the Kelly Criterion leads to higher wealth compared to any other strategy in the long run, it is a scientific gambling method.
In finance, return is a profit on an investment. It comprises any change in value of the investment, and/or cash flows which the investor receives from that investment, such as interest payments, coupons, cash dividends, stock dividends or the payoff from a derivative or structured product. It may be measured either in absolute terms or as a percentage of the amount invested. The latter is also called the holding period return.
Single-loss expectancy (SLE) is the monetary value expected from the occurrence of a risk on an asset. It is related to risk management and risk assessment.

Constant proportion portfolio investment (CPPI) is a trading strategy that allows an investor to maintain an exposure to the upside potential of a risky asset while providing a capital guarantee against downside risk. The outcome of the CPPI strategy is somewhat similar to that of buying a call option, but does not use option contracts. Thus CPPI is sometimes referred to as a convex strategy, as opposed to a "concave strategy" like constant mix.
Exposure assessment is a branch of environmental science and occupational hygiene that focuses on the processes that take place at the interface between the environment containing the contaminant of interest and the organism being considered. These are the final steps in the path to release an environmental contaminant, through transport to its effect in a biological system. It tries to measure how much of a contaminant can be absorbed by an exposed target organism, in what form, at what rate and how much of the absorbed amount is actually available to produce a biological effect. Although the same general concepts apply to other organisms, the overwhelming majority of applications of exposure assessment are concerned with human health, making it an important tool in public health.
The S&P/ASX 300, or simply, ASX 300, is a stock market index of Australian stocks listed on the Australian Securities Exchange (ASX). The index is market-capitalisation weighted, meaning each company included is in proportion to the indexes total market value, and float-adjusted, meaning the index only considers shares available to public investors.
Valuation risk is the risk that an entity suffers a loss when trading an asset or a liability due to a difference between the accounting value and the price effectively obtained in the trade.
The Vanna–Volga method is a mathematical tool used in finance. It is a technique for pricing first-generation exotic options in foreign exchange market (FX) derivatives.

Astronauts are exposed to approximately 50-2,000 millisieverts (mSv) while on six-month-duration missions to the International Space Station (ISS), the Moon and beyond. The risk of cancer caused by ionizing radiation is well documented at radiation doses beginning at 100mSv and above.
Returns-based style analysis is a statistical technique used in finance to deconstruct the returns of investment strategies using a variety of explanatory variables. The model results in a strategy's exposures to asset classes or other factors, interpreted as a measure of a fund or portfolio manager's style. While the model is most frequently used to show an equity mutual fund’s style with reference to common style axes, recent applications have extended the model’s utility to model more complex strategies, such as those employed by hedge funds. Returns based strategies that use factors such as momentum signals have been popular to the extent that industry analysts incorporate their use in their Buy/Sell recommendations.
In mathematical finance, multiple factor models are asset pricing models that can be used to estimate the discount rate for the valuation of financial assets. They are generally extensions of the single-factor capital asset pricing model (CAPM).
In finance, a zero coupon swap (ZCS) is an interest rate derivative (IRD). In particular it is a linear IRD, that in its specification is very similar to the much more widely traded interest rate swap (IRS).






