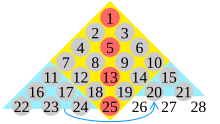
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients arising in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.
19 (nineteen) is the natural number following 18 and preceding 20. It is a prime number.
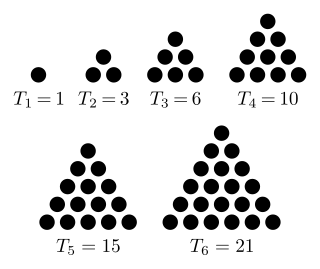
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n. The sequence of triangular numbers, starting with the 0th triangular number, is
90 (ninety) is the natural number following 89 and preceding 91.
72 (seventy-two) is the natural number following 71 and preceding 73. It is half a gross or 6 dozen.

120 is the natural number following 119 and preceding 121.
1000 or one thousand is the natural number following 999 and preceding 1001. In most English-speaking countries, it can be written with or without a comma or sometimes a period separating the thousands digit: 1,000.
666 is the natural number following 665 and preceding 667.
700 is the natural number following 699 and preceding 701.
600 is the natural number following 599 and preceding 601.

In number theory, a pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left. It is named because it represents the number of 3-dimensional unit spheres which can be packed into a pentatope of increasing side lengths.

The lazy caterer's sequence, more formally known as the central polygonal numbers, describes the maximum number of pieces of a disk that can be made with a given number of straight cuts. For example, three cuts across a pancake will produce six pieces if the cuts all meet at a common point inside the circle, but up to seven if they do not. This problem can be formalized mathematically as one of counting the cells in an arrangement of lines; for generalizations to higher dimensions, see arrangement of hyperplanes.
10,000,000 is the natural number following 9,999,999 and preceding 10,000,001.
Lozanić's triangle is a triangular array of binomial coefficients in a manner very similar to that of Pascal's triangle. It is named after the Serbian chemist Sima Lozanić, who researched it in his investigation into the symmetries exhibited by rows of paraffins.
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has garnered attention throughout history in part because distal extremities in humans typically contain five digits.
In combinatorics, the Narayana numbers form a triangular array of natural numbers, called the Narayana triangle, that occur in various counting problems. They are named after Canadian mathematician T. V. Narayana (1930–1987).

In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index. That is, the ith row contains only i elements.

In mathematics, the Bell triangle is a triangle of numbers analogous to Pascal's triangle, whose values count partitions of a set in which a given element is the largest singleton. It is named for its close connection to the Bell numbers, which may be found on both sides of the triangle, and which are in turn named after Eric Temple Bell. The Bell triangle has been discovered independently by multiple authors, beginning with Charles Sanders Peirce (1880) and including also Alexander Aitken (1933) and Cohn et al. (1962), and for that reason has also been called Aitken's array or the Peirce triangle.

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by:

In mathematics, the doubly triangular numbers are the numbers that appear within the sequence of triangular numbers, in positions that are also triangular numbers. That is, if denotes the th triangular number, then the doubly triangular numbers are the numbers of the form .