
In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in number theory. The values of the first 20 Bernoulli numbers are given in the adjacent table. For every even n other than 0, Bn is negative if n is divisible by 4 and positive otherwise. For every odd n other than 1, Bn = 0.

In mathematics, a Cauchy sequence, named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses. More precisely, given any small positive distance, all but a finite number of elements of the sequence are less than that given distance from each other.
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. Mathematically, the logistic map is written
In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no perfect square other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.

Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern. When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
25 (twenty-five) is the natural number following 24 and preceding 26.
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.

In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, only prime numbers are multiplied. The symbol for primorial is “#”.
126 is the natural number following 125 and preceding 127.
In recreational mathematics, a harshad number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers in base n are also known as n-harshad numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The term “Niven number” arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977. All integers between zero and n are n-harshad numbers.
A highly totient number is an integer that has more solutions to the equation , where is Euler's totient function, than any integer below it. The first few highly totient numbers are
In number theory, a smooth (or friable) number is an integer which factors completely into small prime numbers. For example, a 7-smooth number is a number whose prime factors are all at most 7, so 49 = 72 and 15750 = 2 × 32 × 53 × 7 are both 7-smooth, while 11 and 702 = 2 × 33 × 13 are not. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization. The 2-smooth numbers are just the powers of 2, while 5-smooth numbers are known as regular numbers.
In number theory, a branch of mathematics, a highly cototient number is a positive integer which is above 1 and has more solutions to the equation
A cyclic number is an integer in which cyclic permutations of the digits are successive multiples of the number. The most widely known is the six-digit number 142857, whose first six integer multiples are
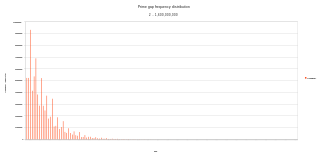
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-th and the n-th prime numbers, i.e.
In mathematics, the Fibonacci numbers form a sequence defined recursively by:
In mathematics, Euler's idoneal numbers are the positive integers D such that any integer expressible in only one way as x2 ± Dy2 is a prime, prime power, twice one of these, or a power of 2. In particular, a number that has two distinct representations as a sum of two squares is composite. Every idoneal number generates a set containing infinitely many primes and missing infinitely many other primes.
In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal and gamma distributions, the purely discrete scaled Poisson distribution, and the class of mixed compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. For any random variable Y that obeys a Tweedie distribution, the variance var(Y) relates to the mean E(Y) by the power law,
In mathematics, Bhargava's factorial function, or simply Bhargava factorial, is a certain generalization of the factorial function developed by the Fields Medal winning mathematician Manjul Bhargava as part of his thesis in Harvard University in 1996. The Bhargava factorial has the property that many number-theoretic results involving the ordinary factorials remain true even when the factorials are replaced by the Bhargava factorials. Using an arbitrary infinite subset S of the set Z of integers, Bhargava associated a positive integer with every positive integer k, which he denoted by k !S, with the property that if we take S = Z itself, then the integer associated with k, that is k !Z, would turn out to be the ordinary factorial of k.
Clark Kimberling is a mathematician, musician, and composer. He has been a mathematics professor since 1970 at the University of Evansville. His research interests include triangle centers, integer sequences, and hymnology.
zbMATH, formerly Zentralblatt MATH, is a major international reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastructure GmbH. Editors are the European Mathematical Society (EMS), FIZ Karlsruhe, and the Heidelberg Academy of Sciences. zbMATH is distributed by Springer Science+Business Media. It uses the Mathematics Subject Classification codes for organising the reviews by topic.








