In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

In calculus, Taylor's theorem gives an approximation of a -times differentiable function around a given point by a polynomial of degree , called the -th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:
In mathematics, an Appell sequence, named after Paul Émile Appell, is any polynomial sequence satisfying the identity
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology (named after Pierre Dolbeault) is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold. Then the Dolbeault cohomology groups depend on a pair of integers p and q and are realized as a subquotient of the space of complex differential forms of degree (p,q).
In mathematics, in the area of complex analysis, the general difference polynomials are a polynomial sequence, a certain subclass of the Sheffer polynomials, which include the Newton polynomials, Selberg's polynomials, and the Stirling interpolation polynomials as special cases.
In combinatorial mathematics, the q-difference polynomials or q-harmonic polynomials are a polynomial sequence defined in terms of the q-derivative. They are a generalized type of Brenke polynomial, and generalize the Appell polynomials. See also Sheffer sequence.

In mathematics, the Chebyshev function is either a scalarising function (Tchebycheff function) or one of two related functions. The first Chebyshev functionϑ (x) or θ (x) is given by

This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.
In mathematical analysis, and especially in real, harmonic analysis and functional analysis, an Orlicz space is a type of function space which generalizes the Lp spaces. Like the Lp spaces, they are Banach spaces. The spaces are named for Władysław Orlicz, who was the first to define them in 1932.
In discrete calculus the indefinite sum operator, denoted by or , is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus
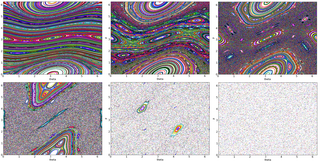
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian
In the science of fluid flow, Stokes' paradox is the phenomenon that there can be no creeping flow of a fluid around a disk in two dimensions; or, equivalently, the fact there is no non-trivial steady-state solution for the Stokes equations around an infinitely long cylinder. This is opposed to the 3-dimensional case, where Stokes' method provides a solution to the problem of flow around a sphere.
The Fuchsian theory of linear differential equations, which is named after Lazarus Immanuel Fuchs, provides a characterization of various types of singularities and the relations among them.
The Bernoulli polynomials of the second kindψn(x), also known as the Fontana-Bessel polynomials, are the polynomials defined by the following generating function:
Tau functions are an important ingredient in the modern mathematical theory of integrable systems, and have numerous applications in a variety of other domains. They were originally introduced by Ryogo Hirota in his direct method approach to soliton equations, based on expressing them in an equivalent bilinear form.



































