Glasser's master theorem

Last updated April 04, 2019

In integral calculus, Glasser's master theorem explains how a certain broad class of substitutions can simplify certain integrals over the whole interval from $-\infty$ to $+\infty .$ It is applicable in cases where the integrals must be construed as Cauchy principal values, and a fortiori it is applicable when the integral converges absolutely. It is named after M. L. Glasser, who introduced it in 1983.^[1]

In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.

In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series $is said to converge absolutely if for some real number . Similarly, an improper integral of a function,, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if$

A special case: the Cauchy–Schlömilch transformation

A special case called the Cauchy–Schlömilch substitution or Cauchy–Schlömilch transformation^[2] was known to Cauchy in the early 19th century.^[3] It states that if

Baron Augustin-Louis Cauchy was a French mathematician, engineer and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra.

u=x-{\frac {1}{x}}\,

then

\operatorname {PV} \int _{-\infty }^{\infty }F(u)\,dx=\operatorname {PV} \int _{-\infty }^{\infty }F(x)\,dx\qquad ({\text{Note: }}F(u)\,dx,{\text{ not }}F(u)\,du)

where PV denotes the Cauchy principal value.

The master theorem

If $a$ , $a_{i}$ , and $b_{i}$ are real numbers and

u=x-a-\sum _{n=1}^{N}{\frac {|a_{n}|}{x-b_{n}}}

then

\operatorname {PV} \int _{-\infty }^{\infty }F(u)\,dx=\operatorname {PV} \int _{-\infty }^{\infty }F(x)\,dx.

Examples

$\int _{-\infty }^{\infty }{\frac {x^{2}\,dx}{x^{4}+1}}=\int _{-\infty }^{\infty }{\frac {dx}{\left(x-{\frac {1}{x}}\right)^{2}+2}}=\int _{-\infty }^{\infty }{\frac {dx}{x^{2}+2}}={\frac {\pi }{\sqrt {2}}}.$

Related Research Articles

The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution, Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution $is the distribution of the x -intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables if the denominator distribution has mean zero.$

In probability theory, the expected value of a random variable, intuitively, is the long-run average value of repetitions of the same experiment it represents. For example, the expected value in rolling a six-sided die is 3.5, because the average of all the numbers that come up is 3.5 as the number of rolls approaches infinity. In other words, the law of large numbers states that the arithmetic mean of the values almost surely converges to the expected value as the number of repetitions approaches infinity. The expected value is also known as the expectation, mathematical expectation, EV, average, mean value, mean, or first moment.

In mathematics, the Laplace transform is an integral transform named after its inventor Pierre-Simon Laplace. It takes a function of a real variable $t$ to a function of a complex variable $s$ . The transform has many applications in science and engineering.

In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

In complex analysis, a discipline within mathematics, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. From a geometrical perspective, it is a special case of the generalized Stokes' theorem.

In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be readily derived by integrating the product rule of differentiation.

Integration is the basic operation in integral calculus. While differentiation has easy rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C. It is named after George Green, though its first proof is due to Bernhard Riemann and is the two-dimensional special case of the more general Kelvin–Stokes theorem.

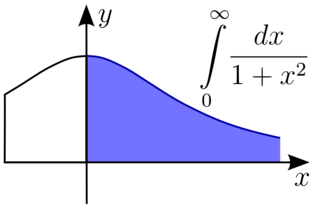
Improper integral Limit of a definite integral with as one or both limits approach infinity or values at which the integrand is undefined

In mathematical analysis, an improper integral is the limit of a definite integral as an endpoint of the interval(s) of integration approaches either a specified real number, $,, or in some instances as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, in some cases with infinity as a limit of integration.$

In mathematics, the Riemann–Liouville integral associates with a real function ƒ : R → R another function I^αƒ of the same kind for each value of the parameter α > 0. The integral is a manner of generalization of the repeated antiderivative of ƒ in the sense that for positive integer values of α, I^αƒ is an iterated antiderivative of ƒ of order α. The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential.

In mathematics, a Paley–Wiener theorem is any theorem that relates decay properties of a function or distribution at infinity with analyticity of its Fourier transform. The theorem is named for Raymond Paley (1907–1933) and Norbert Wiener (1894–1964). The original theorems did not use the language of distributions, and instead applied to square-integrable functions. The first such theorem using distributions was due to Laurent Schwartz.

In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.

In calculus, interchange of the order of integration is a methodology that transforms iterated integrals of functions into other, hopefully simpler, integrals by changing the order in which the integrations are performed. In some cases, the order of integration can be validly interchanged; in others it cannot.

In mathematics, Ramanujan's master theorem is a technique that provides an analytic expression for the Mellin transform of an analytic function.

The Fokas method, or unified transform, is an algorithmic procedure for analysing boundary value problems for linear partial differential equations and for an important class of nonlinear PDEs belonging to the so-called integrable systems. It is named after Greek mathematician Athanassios S. Fokas.

References

↑ Glasser, M. L. "A Remarkable Property of Definite Integrals." Mathematics of Computation 40, 561–563, 1983.
↑ T. Amdeberhnan, M. L. Glasser, M. C. Jones, V. H. Moll, R. Posey, and D. Varela, "The Cauchy–Schlömilch transformation", arxiv.org/pdf/1004.2445.pdf
↑ A. L. Cauchy, "Sur une formule generale relative a la transformation des integrales simples prises entre les limites 0 et ∞ de la variable." Oeuvres completes, serie 2, Journal de l’ecole Polytechnique, XIX cahier, tome XIII, 516–519, 1:275–357, 1823

External links

Weisstein, Eric W. "Glasser's Master Theorem". MathWorld .

Eric Wolfgang Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science (ScienceWorld). He is the author of the CRC Concise Encyclopedia of Mathematics. He currently works for Wolfram Research, Inc.

MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Glasser, M. L. "A Remarkable Property of Definite Integrals." Mathematics of Computation 40, 561–563, 1983.

[2] T. Amdeberhnan, M. L. Glasser, M. C. Jones, V. H. Moll, R. Posey, and D. Varela, "The Cauchy–Schlömilch transformation", arxiv.org/pdf/1004.2445.pdf

[3] A. L. Cauchy, "Sur une formule generale relative a la transformation des integrales simples prises entre les limites 0 et ∞ de la variable." Oeuvres completes, serie 2, Journal de l’ecole Polytechnique, XIX cahier, tome XIII, 516–519, 1:275–357, 1823