
In atomic physics, the Bohr model or Rutherford–Bohr model, presented by Niels Bohr and Ernest Rutherford in 1913, is a system consisting of a small, dense nucleus surrounded by orbiting electrons—similar to the structure of the Solar System, but with attraction provided by electrostatic forces in place of gravity. After the solar system Joseph Larmor model (1897), the cubical model (1902), the Hantaro Nagaoka Saturnian model (1904), the plum pudding model (1904), the quantum Arthur Haas model (1910), the Rutherford model (1911), and the nuclear quantum John William Nicholson model (1912), came the Rutherford–Bohr model or just Bohr model for short (1913). The improvement over the 1911 Rutherford model mainly concerned the new quantum physical interpretation introduced by Haas and Nicholson, but forsaking any attempt to align with classical physics radiation.
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy.
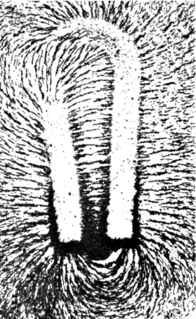
Magnetic field is a vector field that describes interaction between moving electric charges, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a magnetic field that varies with location will exert a force on a range of non-magnetic materials by affecting the motion of their outer atomic electrons. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe, as well as classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists around the world, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, confirmation of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

A bipolar junction transistor (BJT) is a type of transistor that uses both electrons and electron holes as charge carriers. In contrast, a unipolar transistor, such as a field-effect transistor, uses only one kind of charge carrier. A bipolar transistor allows a small current injected at one of its terminals to control a much larger current flowing between the terminals, making the device capable of amplification or switching.
Ionization or ionisation is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule is called an ion. Ionization can result from the loss of an electron after collisions with subatomic particles, collisions with other atoms, molecules and ions, or through the interaction with electromagnetic radiation. Heterolytic bond cleavage and heterolytic substitution reactions can result in the formation of ion pairs. Ionization can occur through radioactive decay by the internal conversion process, in which an excited nucleus transfers its energy to one of the inner-shell electrons causing it to be ejected.
Hidden Markov Model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process — call it — with unobservable ("hidden") states. As part of the definition, HMM requires that there be an observable process whose outcomes are "influenced" by the outcomes of in a known way. Since cannot be observed directly, the goal is to learn about by observing HMM has an additional requirement that the outcome of at time may be "influenced" exclusively by the outcome of at and that the outcomes of and at must not affect the outcome of at

The Ford Mustang is a series of American automobiles manufactured by Ford. In continuous production since 1964, the Mustang is currently the longest-produced Ford car nameplate. Currently in its sixth generation, it is the fifth-best selling Ford car nameplate. The namesake of the "pony car" automobile segment, the Mustang was developed as a highly styled line of sporty coupes and convertibles derived from existing model lines, initially distinguished by "long hood, short deck" proportions.
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.
In statistics, the logistic model is used to model the probability of a certain class or event taking place, such as the probability of a team winning, of a patient being healthy, etc. This can be extended to model several classes of events such as determining whether an image contains a cat, dog, lion, etc. Each object being detected in the image would be assigned a probability between 0 and 1, with a sum of one.

HSL and HSV are alternative representations of the RGB color model, designed in the 1970s by computer graphics researchers to more closely align with the way human vision perceives color-making attributes. In these models, colors of each hue are arranged in a radial slice, around a central axis of neutral colors which ranges from black at the bottom to white at the top.

In biochemistry, Michaelis–Menten kinetics is one of the best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating reaction rate to , the concentration of a substrate S. Its formula is given by
The Ising model, , named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.

The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed.
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable and one or more independent variables. The most common form of regression analysis is linear regression, in which one finds the line that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line that minimizes the sum of squared differences between the true data and that line. For specific mathematical reasons, this allows the researcher to estimate the conditional expectation of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters or estimate the conditional expectation across a broader collection of non-linear models.
Pharmacokinetics, sometimes abbreviated as PK, is a branch of pharmacology dedicated to determine the fate of substances administered to a living organism. The substances of interest include any chemical xenobiotic such as: pharmaceutical drugs, pesticides, food additives, cosmetics, etc. It attempts to analyze chemical metabolism and to discover the fate of a chemical from the moment that it is administered up to the point at which it is completely eliminated from the body. Pharmacokinetics is the study of how an organism affects a drug, whereas pharmacodynamics (PD) is the study of how the drug affects the organism. Both together influence dosing, benefit, and adverse effects, as seen in PK/PD models.
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables. The case of one explanatory variable is called simple linear regression; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.








