
In the field of complex analysis in mathematics, the Cauchy–Riemann equations, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which, together with certain continuity and differentiability criteria, form a necessary and sufficient condition for a complex function to be complex differentiable, that is, holomorphic. This system of equations first appeared in the work of Jean le Rond d'Alembert. Later, Leonhard Euler connected this system to the analytic functions. Cauchy (1814) then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is indifferent. That is, the consumer has no preference for one combination or bundle of goods over a different combination on the same curve. One can also refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words, an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferences rather than something from which preferences come. The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles.

The moment of inertia, otherwise known as the angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis; similar to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rotation rate. It is an extensive (additive) property: for a point mass the moment of inertia is just the mass times the square of the perpendicular distance to the rotation axis. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems. Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3 × 3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other.
In mathematics, the Kronecker delta is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
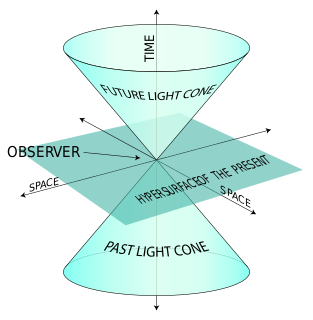
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy E and three-momentum p = = γmv, where v is the particle's three-velocity and γ the Lorentz factor, is
Price elasticity of demand is a measure used in economics to show the responsiveness, or elasticity, of the quantity demanded of a good or service to a change in its price when nothing but the price changes. More precisely, it gives the percentage change in quantity demanded in response to a one percent change in price.

The stream function is defined for incompressible (divergence-free) flows in two dimensions – as well as in three dimensions with axisymmetry. The flow velocity components can be expressed as the derivatives of the scalar stream function. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. The two-dimensional Lagrange stream function was introduced by Joseph Louis Lagrange in 1781. The Stokes stream function is for axisymmetrical three-dimensional flow, and is named after George Gabriel Stokes.
The theory of consumer choice is the branch of microeconomics that relates preferences to consumption expenditures and to consumer demand curves. It analyzes how consumers maximize the desirability of their consumption as measured by their preferences subject to limitations on their expenditures, by maximizing utility subject to a consumer budget constraint.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

A substitute good is a good that can be used in place of another. In consumer theory, substitute goods or substitutes are products that a consumer perceives as similar or comparable, so that having more of one product makes them desire less of the other product. Formally, X and Y are substitutes if, when the price of X rises, the demand for Y rises.

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.

In economics and in particular neoclassical economics, the marginal product or marginal physical productivity of an input is the change in output resulting from employing one more unit of a particular input, assuming that the quantities of other inputs are kept constant.
In microeconomics, a consumer's Marshallian demand function specifies what the consumer would buy in each price and income or wealth situation, assuming it perfectly solves the utility maximization problem. Marshallian demand is sometimes called Walrasian demand or uncompensated demand function instead, because the original Marshallian analysis refused wealth effects.
In economics, an ordinal utility function is a function representing the preferences of an agent on an ordinal scale. The ordinal utility theory claims that it is only meaningful to ask which option is better than the other, but it is meaningless to ask how much better it is or how good it is. All of the theory of consumer decision-making under conditions of certainty can be, and typically is, expressed in terms of ordinal utility.
Competitive equilibrium is the traditional concept of economic equilibrium, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated.
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846.
In economics, income elasticity of demand measures the responsiveness of the quantity demanded for a good or service to a change in income. It is calculated as the ratio of the percentage change in quantity demanded to the percentage change in income. For example, if in response to a 10% increase in income, the quantity demanded for a good increased by 20%, the income elasticity of demand would be 20%/10% = 2.0.
Minimalist grammars are a class of formal grammars that aim to provide a more rigorous, usually proof-theoretic, formalization of Chomskyan Minimalist program than is normally provided in the mainstream Minimalist literature. A variety of particular formalizations exist, most of them developed by Edward Stabler, Alain Lecomte, Christian Retoré, or combinations thereof.
A two-dimensional conformal field theory is a quantum field theory on a Euclidean two-dimensional space, that is invariant under local conformal transformations.












