
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.

In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
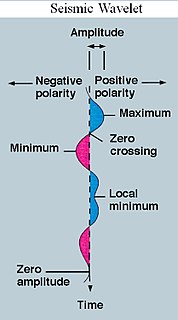
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
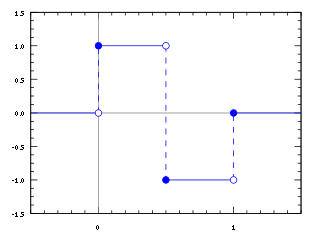
In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example.

A Fourier transform (FT) is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial frequency or temporal frequency. That process is also called analysis. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time.

A Fourier series is a sum that represents a periodic function as a sum of sine and cosine waves. The frequency of each wave in the sum, or harmonic, is an integer multiple of the periodic function's fundamental frequency. Each harmonic's phase and amplitude can be determined using harmonic analysis. A Fourier series may potentially contain an infinite number of harmonics. Summing part of but not all the harmonics in a function's Fourier series produces an approximation to that function. For example, using the first few harmonics of the Fourier series for a square wave yields an approximation of a square wave.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.

The Short-time Fourier transform (STFT), is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. In practice, the procedure for computing STFTs is to divide a longer time signal into shorter segments of equal length and then compute the Fourier transform separately on each shorter segment. This reveals the Fourier spectrum on each shorter segment. One then usually plots the changing spectra as a function of time, known as a spectrogram or waterfall plot, such as commonly used in Software Defined Radio (SDR) based spectrum displays. Full bandwidth displays covering the whole range of an SDR commonly use Fast Fourier Transforms (FFTs) with 2^24 points on desktop computers.
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples of the original function's Fourier transform. And conversely, the periodic summation of a function's Fourier transform is completely defined by discrete samples of the original function. The Poisson summation formula was discovered by Siméon Denis Poisson and is sometimes called Poisson resummation.
In the theory of stochastic processes, the Karhunen–Loève theorem, also known as the Kosambi–Karhunen–Loève theorem is a representation of a stochastic process as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function on a bounded interval. The transformation is also known as Hotelling transform and eigenvector transform, and is closely related to principal component analysis (PCA) technique widely used in image processing and in data analysis in many fields.
In mathematics, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.

In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables.
In mathematics, the secondary measure associated with a measure of positive density ρ when there is one, is a measure of positive density μ, turning the secondary polynomials associated with the orthogonal polynomials for ρ into an orthogonal system.
In mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra. It is a natural generalisation in non-commutative harmonic analysis of the Plancherel formula and Fourier inversion formula in the representation theory of the group of real numbers in classical harmonic analysis and has a similarly close interconnection with the theory of differential equations. It is the special case for zonal spherical functions of the general Plancherel theorem for semisimple Lie groups, also proved by Harish-Chandra. The Plancherel theorem gives the eigenfunction expansion of radial functions for the Laplacian operator on the associated symmetric space X; it also gives the direct integral decomposition into irreducible representations of the regular representation on L2(X). In the case of hyperbolic space, these expansions were known from prior results of Mehler, Weyl and Fock.
In mathematics, the Neumann–Poincaré operator or Poincaré–Neumann operator, named after Carl Neumann and Henri Poincaré, is a non-self-adjoint compact operator introduced by Poincaré to solve boundary value problems for the Laplacian on bounded domains in Euclidean space. Within the language of potential theory it reduces the partial differential equation to an integral equation on the boundary to which the theory of Fredholm operators can be applied. The theory is particularly simple in two dimensions—the case treated in detail in this article—where it is related to complex function theory, the conjugate Beurling transform or complex Hilbert transform and the Fredholm eigenvalues of bounded planar domains.
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96. In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel. In still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.

Phase stretch transform (PST) is a computational approach to signal and image processing. One of its utilities is for feature detection and classification. PST is related to time stretch dispersive Fourier transform. It transforms the image by emulating propagation through a diffractive medium with engineered 3D dispersive property. The operation relies on symmetry of the dispersion profile and can be understood in terms of dispersive eigenfunctions or stretch modes. PST performs similar functionality as phase-contrast microscopy, but on digital images. PST can be applied to digital images and temporal data. It is a physics-based feature engineering algorithm.
Linear expansions in a single basis, whether it is a Fourier series, wavelet, or any other basis, are not suitable enough. A Fourier basis provided a poor representation of functions well localized in time, and wavelet bases are not well adapted to represent functions whose Fourier transforms have a narrow high frequency support. In both cases, it is difficult to detect and identify the signal patterns from their expansion coefficients, because the information is diluted across the whole basis. Therefore, we must use large amounts of Fourier basis or Wavelets to represent whole signal with small approximation error. Some matching pursuit algorithms are proposed in reference papers to minimize approximation error when given the amount of basis.
Multiresolution Fourier Transform is an integral fourier transform that represents a specific wavelet-like transform with a fully scalable modulated window, but not all possible translations.



























