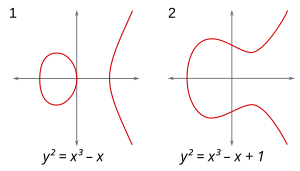
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz. Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines.
The fundamental theorem of algebra, also known as d'Alembert's theorem, or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.
In mathematics, the Weil conjectures were highly influential proposals by André Weil (1949). They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
In mathematics, the operator norm measures the "size" of certain linear operators by assigning each a real number called its operator norm. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.
The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeros and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function for which there exists a positive number such that for all in is constant. Equivalently, non-constant holomorphic functions on have unbounded images.
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, as part of his list of 23 problems in mathematics.
In mathematics, a Cohen–Macaulay ring is a commutative ring with some of the algebro-geometric properties of a smooth variety, such as local equidimensionality. Under mild assumptions, a local ring is Cohen–Macaulay exactly when it is a finitely generated free module over a regular local subring. Cohen–Macaulay rings play a central role in commutative algebra: they form a very broad class, and yet they are well understood in many ways.
In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix.
In the mathematical fields of partial differential equations and geometric analysis, the maximum principle is any of a collection of results and techniques of fundamental importance in the study of elliptic and parabolic differential equations.

In mathematics, the real coordinate space of dimension n, denoted Rn or , is the set of the n-tuples of real numbers, that is the set of all sequences of n real numbers. With component-wise addition and scalar multiplication, it is a real vector space, and its elements are called coordinate vectors.

Critical point is a wide term used in many branches of mathematics.
In the mathematical discipline of functional analysis, the concept of a compact operator on Hilbert space is an extension of the concept of a matrix acting on a finite-dimensional vector space; in Hilbert space, compact operators are precisely the closure of finite-rank operators in the topology induced by the operator norm. As such, results from matrix theory can sometimes be extended to compact operators using similar arguments. By contrast, the study of general operators on infinite-dimensional spaces often requires a genuinely different approach.
In mathematics, real algebraic geometry is the sub-branch of algebraic geometry studying real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them.
In algebra and algebraic geometry, given a commutative Noetherian ring and an ideal in it, the n-th symbolic power of is the ideal
This is a glossary for the terminology in a mathematical field of functional analysis.