
A head is one of the end caps on a cylindrically shaped pressure vessel.

A head is one of the end caps on a cylindrically shaped pressure vessel.
Vessel dished ends are mostly used in storage or pressure vessels in industry. These ends, which in upright vessels are the bottom and the top, use less space than a hemisphere (which is the ideal form for pressure containments) while requiring only a slightly thicker wall.
The manufacturing of such an end is easier than that of a hemisphere. The starting material is first pressed to a radius r1 and then curled at the edge creating the second radius r2. Vessel dished ends can also be welded together from smaller pieces.
The shape of the heads used can vary. The most common [1] [2] head shapes are:
A sphere is the ideal shape for a head, because the stresses are distributed evenly through the material of the head. The radius (r) of the head equals the radius of the cylindrical part of the vessel.
This is also called an elliptical head. The shape of this head is more economical, because the height of the head is just a fraction of the diameter. Its radius varies between the major and minor axis; usually the ratio is 2:1.
These heads have a dish with a fixed radius (r1), the size of which depends on the type of torispherical head. [3] The transition between the cylinder and the dish is called the knuckle. The knuckle has a toroidal shape. The most common types of torispherical heads are:
Commonly used for ASME pressure vessels, these torispherical heads have a crown radius equal to the outside diameter of the head (), and a knuckle radius equal to 6% of the outside diameter (). The ASME design code does not allow the knuckle radius to be any less than 6% of the outside diameter. [4]

This is a torispherical head. The dish has a radius that equals the diameter of the cylinder it is attached to (). The knuckle has a radius that equals a tenth of the diameter of the cylinder (), hence its alternative designation "decimal head".
This is a torispherical head also named Semi ellipsoidal head (According to DIN 28013). The radius of the dish is 80% of the diameter of the cylinder (). The radius of the knuckle is ().
These heads have a crown radius of 80% of outside diameter, and a knuckle radius of 10% of outside diameter.
This is a head consisting of a toroidal knuckle connecting to a flat plate. This type of head is typically used for the bottom of cookware.


This type of head is often found on the bottom of aerosol spray cans. It is an inverted torispherical head.
This is a cone-shaped head.
Heat treatment may be required after cold forming, but not for heads formed by hot forming. [7]

A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

A sphere is a perfectly round geometrical object in three-dimensional space that is the surface of a completely round ball.

Volume is the quantity of three-dimensional space enclosed by a closed surface, for example, the space that a substance or shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. The volume of a container is generally understood to be the capacity of the container; i. e., the amount of fluid that the container could hold, rather than the amount of space the container itself displaces. Three dimensional mathematical shapes are also assigned volumes. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space.
Hemodynamics or haemodynamics are the dynamics of blood flow. The circulatory system is controlled by homeostatic mechanisms, such as hydraulic circuits are controlled by control systems. Hemodynamic response continuously monitors and adjusts to conditions in the body and its environment. Thus hemodynamics explains the physical laws that govern the flow of blood in the blood vessels.

A pressure vessel is a container designed to hold gases or liquids at a pressure substantially different from the ambient pressure.
Vascular resistance is the resistance that must be overcome to push blood through the circulatory system and create flow. The resistance offered by the systemic circulation is known as the systemic vascular resistance (SVR) or may sometimes be called by the older term total peripheral resistance (TPR), while the resistance offered by the pulmonary circulation is known as the pulmonary vascular resistance (PVR). Systemic vascular resistance is used in calculations of blood pressure, blood flow, and cardiac function. Vasoconstriction increases SVR, whereas vasodilation decreases SVR.

Rolling resistance, sometimes called rolling friction or rolling drag, is the force resisting the motion when a body rolls on a surface. It is mainly caused by non-plastic effects; that is, not all the energy needed for deformation of the wheel, roadbed, etc. is recovered when the pressure is removed. Two forms of this are hysteresis losses, and permanent (plastic) deformation of the object or the surface. Another cause of rolling resistance lies in the slippage between the wheel and the surface, which dissipates energy. Note that only the last of these effects involves friction, therefore the name "rolling friction" is to an extent a misnomer.

In mechanics, a cylinder stress is a stress distribution with rotational symmetry; that is, which remains unchanged if the stressed object is rotated about some fixed axis.
Given the problem of the aerodynamic design of the nose cone section of any vehicle or body meant to travel through a compressible fluid medium, an important problem is the determination of the nose cone geometrical shape for optimum performance. For many applications, such a task requires the definition of a solid of revolution shape that experiences minimal resistance to rapid motion through such a fluid medium, which consists of elastic particles.
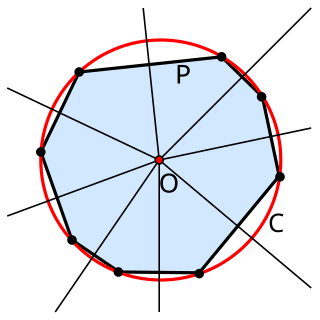
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle O of radius r is defined by.

Pneumatic cylinder(s) are mechanical devices which use the power of compressed gas to produce a force in a reciprocating linear motion.

Torricelli's law, also known as Torricelli's theorem, is a theorem in fluid dynamics relating the speed of fluid flowing from an orifice to the height of fluid above the opening. The law states that the speed v of efflux of a fluid through a sharp-edged hole at the bottom of a tank filled to a depth h is the same as the speed that a body would acquire in falling freely from a height h, i.e. , where g is the acceleration due to gravity. This expression comes from equating the kinetic energy gained, , with the potential energy lost, mgh, and solving for v. The law was discovered by the Italian scientist Evangelista Torricelli, in 1643. It was later shown to be a particular case of Bernoulli's principle.

A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the cylindrical sides of the tube are everywhere parallel to the magnetic field lines. It is a graphical visual aid for visualizing a magnetic field. Since no magnetic flux passes through the sides of the tube, the flux through any cross section of the tube is equal, and the flux entering the tube at one end is equal to the flux leaving the tube at the other. Both the cross-sectional area of the tube and the magnetic field strength may vary along the length of the tube, but the magnetic flux inside is always constant.
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.

In geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height.

In a toroidal fusion power reactor, the magnetic fields confining the plasma are formed in a helical shape, winding around the interior of the reactor. The safety factor, labeled q or q(r), is the ratio of the times a particular magnetic field line travels around a toroidal confinement area's "long way" (toroidally) to the "short way" (poloidally).

Jurin's law, or capillary rise, is the simplest analysis of capillary action—the induced motion of liquids in small channels—and states that the maximum height of a liquid in a capillary tube is inversely proportional to the tube's diameter. Capillary action is one of the most common fluid mechanical effects explored in the field of microfluidics. Jurin's law is named after James Jurin, who discovered it between 1718 and 1719. His quantitative law suggests that the maximum height of liquid in a capillary tube is inversely proportional to the tube's diameter. The difference in height between the surroundings of the tube and the inside, as well as the shape of the meniscus, are caused by capillary action. The mathematical expression of this law can be derived directly from hydrostatic principles and the Young–Laplace equation. Jurin's law allows the measurement of the surface tension of a liquid and can be used to derive the capillary length.
Bearing pressure is a particular case of contact mechanics often occurring in cases where a convex surface contacts a concave surface. Excessive contact pressure can lead to a typical bearing failure such as a plastic deformation similar to peening. This problem is also referred to as bearing resistance.