Heine's identity

Last updated February 07, 2022

In mathematical analysis, Heine's identity, named after Heinrich Eduard Heine ^[1] is a Fourier expansion of a reciprocal square root which Heine presented as

{\frac {1}{\sqrt {z-\cos \psi }}}={\frac {\sqrt {2}}{\pi }}\sum _{m=-\infty }^{\infty }Q_{m-{\frac {1}{2}}}(z)e^{im\psi }

where^[2] $Q_{m-{\frac {1}{2}}}$ is a Legendre function of the second kind, which has degree, m − 1⁄2, a half-integer, and argument, z, real and greater than one. This expression can be generalized^[3] for arbitrary half-integer powers as follows

(z-\cos \psi )^{n-{\frac {1}{2}}}={\sqrt {\frac {2}{\pi }}}{\frac {(z^{2}-1)^{\frac {n}{2}}}{\Gamma ({\frac {1}{2}}-n)}}\sum _{m=-\infty }^{\infty }{\frac {\Gamma (m-n+{\frac {1}{2}})}{\Gamma (m+n+{\frac {1}{2}})}}Q_{m-{\frac {1}{2}}}^{n}(z)e^{im\psi },

where $\scriptstyle \,\Gamma$ is the Gamma function.

Related Research Articles

Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions $y (x)$ of Bessel's differential equation

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For any positive integer $n$ ,

Eulers constant Relates logarithm and harmonic series

Euler's constant is a mathematical constant usually denoted by the lowercase Greek letter gamma.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other special functions. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.

In mathematics, the polygamma function of order $m$ is a meromorphic function on the complex numbers $defined as the (m + 1) th derivative of the logarithm of the gamma function:$

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, ... by

In mathematics, theta functions are special functions of several complex variables. They are important in many areas, including the theories of Abelian varieties and moduli spaces, and of quadratic forms. They have also been applied to soliton theory. When generalized to a Grassmann algebra, they also appear in quantum field theory.

In mathematics, the Z function is a function used for studying the Riemann zeta function along the critical line where the argument is one-half. It is also called the Riemann–Siegel Z function, the Riemann–Siegel zeta function, the Hardy function, the Hardy Z function and the Hardy zeta function. It can be defined in terms of the Riemann–Siegel theta function and the Riemann zeta function by

In mathematics, the Stieltjes constants are the numbers $that occur in the Laurent series expansion of the Riemann zeta function:$

In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt. It is an example of an important arithmetic function that is neither multiplicative nor additive.

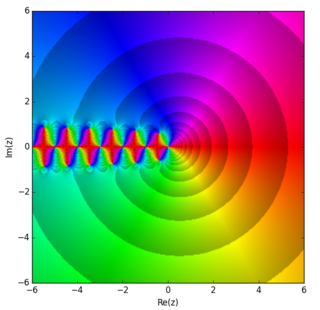
In mathematics, the trigamma function, denoted $ψ 1 (z)$ , is the second of the polygamma functions, and is defined by

In mathematics, particularly $q$ -analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta. The function is named after Srinivasa Ramanujan.

In applied mathematics, the Kelvin functions ber_ν(x) and bei_ν(x) are the real and imaginary parts, respectively, of

In the theory of special functions, Whipple's transformation for Legendre functions, named after Francis John Welsh Whipple, arise from a general expression, concerning associated Legendre functions. These formulae have been presented previously in terms of a viewpoint aimed at spherical harmonics, now that we view the equations in terms of toroidal coordinates, whole new symmetries of Legendre functions arise.

In mathematics the indefinite sum operator, denoted by $or, is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus$

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.

In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.

The Bernoulli polynomials of the second kind $ψ n (x)$ , also known as the Fontana-Bessel polynomials, are the polynomials defined by the following generating function:

References

↑ Heine, Heinrich Eduard (1881). Handbuch der Kugelfunctionen, Theorie und Andwendungen. Wuerzburg: Physica-Verlag.(See page 286)
↑ Cohl, Howard S.; J.E. Tohline; A.R.P. Rau; H.M. Srivastava (2000). "Developments in determining the gravitational potential using toroidal functions". Astronomische Nachrichten . 321 (5/6): 363–372. Bibcode:2000AN....321..363C. doi:10.1002/1521-3994(200012)321:5/6<363::AID-ASNA363>3.0.CO;2-X. ISSN 0004-6337.
↑ Cohl, H. S. (2003). "Portent of Heine's Reciprocal Square Root Identity". 3D Stellar Evolution, ASP Conference Proceedings, held 22-26 July 2002 at University of California Davis, Livermore, California, USA. Edited by Sylvain Turcotte, Stefan C. Keller and Robert M. Cavallo. Vol. 293. ISBN 1-58381-140-0.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Heine, Heinrich Eduard (1881). Handbuch der Kugelfunctionen, Theorie und Andwendungen. Wuerzburg: Physica-Verlag.(See page 286)

[2] Cohl, Howard S.; J.E. Tohline; A.R.P. Rau; H.M. Srivastava (2000). "Developments in determining the gravitational potential using toroidal functions". Astronomische Nachrichten . 321 (5/6): 363–372. Bibcode:2000AN....321..363C. doi:10.1002/1521-3994(200012)321:5/6<363::AID-ASNA363>3.0.CO;2-X. ISSN 0004-6337.

[3] Cohl, H. S. (2003). "Portent of Heine's Reciprocal Square Root Identity". 3D Stellar Evolution, ASP Conference Proceedings, held 22-26 July 2002 at University of California Davis, Livermore, California, USA. Edited by Sylvain Turcotte, Stefan C. Keller and Robert M. Cavallo. Vol. 293. ISBN 1-58381-140-0.

[1]

[2]

[3]