ID/LP grammar

ID/LP Grammars are a subset of Phrase Structure Grammars, differentiated from other formal grammars by distinguishing between immediate dominance (ID) and linear precedence (LP) constraints. Whereas traditional phrase structure rules incorporate dominance and precedence into a single rule, ID/LP Grammars maintains separate rule sets which need not be processed simultaneously. ID/LP Grammars are used in Computational Linguistics.

For example, a typical phrase structure rule such as ${\displaystyle {\ce {S -> NP \; VP}}}$, indicating that an S-node dominates an NP-node and a VP-node, and that the NP precedes the VP in the surface string. In ID/LP Grammars, this rule would only indicate dominance, and a linear precedence statement, such as ${\displaystyle NP\prec VP}$, would also be given.

The idea first came to prominence as part of Generalized Phrase Structure Grammar; ^{[1] [2]} the ID/LP Grammar approach is also used in head-driven phrase structure grammar, ^[3] lexical functional grammar, and other unification grammars.

Current work in the Minimalist Program also attempts to distinguish between dominance and ordering. For instance, recent papers by Noam Chomsky have proposed that, while hierarchical structure is the result of the syntactic structure-building operation Merge, linear order is not determined by this operation, and is simply the result of externalization (oral pronunciation, or, in the case of sign language, manual signing). ^{[4] [5] [6]}

Defining Dominance and Precedence

Immediate Dominance

Immediate dominance is the asymmetrical relationship between the mother node of a parse tree and its daughters, where the mother node (to the left of the arrow) is said to immediately dominate the daughter nodes (those to the right of the arrow), but the daughters do not immediately dominate the mother. The daughter nodes are also dominated by any node that immediately dominates the mother node, however this is not an immediate dominance relation.

For example, the context free rule ${\displaystyle A\rightarrow B\ C\ D}$, shows that the node labelled A (mother node) immediately dominates nodes labelled B, C, and D, (daughter nodes) and nodes labelled B, C, and D can be immediately dominated by a node labelled A.

The node labelled A immediately dominates the nodes B, C, and D, and the node labelled B immediately dominates C' and D'. A also dominates C' and D', but not immediately

Linear Precedence

Linear precedence is the order relationship of sister nodes. LP constraints specify in what order sister nodes under the same mother can appear. Nodes that surface earlier in strings precede their sisters. ^[2] LP can be shown in phrase structure rules in the form ${\displaystyle A\rightarrow B\ C\ D}$ to mean B precedes C precedes D, as shown in the tree below.

A rule that has ID constraints but not LP is written with commas between the daughter nodes, for example ${\displaystyle A\rightarrow B,\ C,\ D}$. Since there is no fixed order for the daughter nodes, it is possible that all three of the trees shown here are generated by this rule.

Alternatively, these relationships can be expressed through linear precedence statements, such as ${\displaystyle B\prec C}$, to mean that anytime B and C are sisters, B must precede C. ^{[2] [7]}

The principle of transitivity can be applied to LP relations which means that if ${\displaystyle B\prec C}$ and ${\displaystyle C\prec D}$, then ${\displaystyle B\prec D}$ as well. LP relationships are asymmetric: if B precedes C, C can never precede B. An LP relationship where there can be no intervening nodes is called immediate precedence, while an LP where there can be intervening nodes (those derived from the principle of transitivity) are said to have weak precedence. ^[8]

Grammaticality in ID/LP Grammars

For a string to be grammatical in an ID/LP Grammar, it must belong to a local subtree that follows at least one ID rule and all LP statements of the grammar. If every possible string generated by the grammar fits this criterion, than it is an ID/LP Grammar. Additionally, for a grammar to be able to be written in ID/LP format, it must have the property of Exhaustive Constant Partial Ordering (ECPO): namely that at least part of the ID/LP relations in one rule is observed in all other rules. ^[2] For example, the set of rules:

(1)${\displaystyle A\rightarrow B\ C\ D}$

(2)${\displaystyle B\rightarrow D\ C\ A}$

does not have the ECPO property, because (1) says that C must always precede D, while (2) says that D must always precede C.

Advantages of ID/LP Grammars

Since LP statements apply regardless of the ID rule context, they allow us to make generalizations across the whole grammar. ^{[2] [7]} For example, given the LP statement ${\displaystyle V\prec DP}$ , where V is the head of a VP, this means that in any clause in any sentence, V will always surface before its DP sister ^[7] in any context, as seen in the following examples.

Lucy won the race.

Ava told Sara to read a book.

This can be generalized into a rule that holds across English, ${\displaystyle X\prec YP}$, where X is the head of any phrase and YP is its complement. Non-ID/LP Grammars are unable to make such generalizations across the whole grammar, and so must repeat ordering restrictions for each individual context. ^[7]

Separating LP requirements from ID rules also accounts for the phenomena of free word order in natural language. For example, in English it is possible to put adverbs before or after a verb and have both strings be grammatical. ^[7]

John suddenly screamed.John screamed suddenly.

A traditional PS rule would require two separate rules, but this can be described by the single ID/LP rule ${\displaystyle VP\rightarrow V,AdvP}$.This property of ID/LP Grammars enables easier cross linguistic generalizations by describing the language specific differences in constituent order with LP statements, separately from the ID rules that are similar across languages. ^[7]

Parsing in ID/LP Grammars

Two parsing algorithms used to parse ID/LP Grammars are the Earley Parser and Shieber's algorithm. ^[9]

Earley Parser in ID/LP Grammars

ID and LP rules impose constraints on sentence strings; ^[9] when dealing with large strings, ^[9] the constraints of these rules can cause the parsed string to become infinite, thus making parsing difficult. The Earley Parser solves this by altering ^[10] the format of an ID/LP Grammar into a Context Free Grammar (CFG), dividing the ID/LP Grammar into an Ordered Context Free Grammar (CFG) and Unordered Context Free Grammar (UCFG). This allows the two algorithms to parse strings more efficiently; ^[9] in particular, the Earley Parser uses a point tracking method that follows a linear path established by the LP rules. ^[9] In a CFG, LP rules do not allow repeated constituents in the parsed string, but an UCFG allows repeated constituents within the parsed strings. ^[9] If the ID/LP Grammar is converted to a UCFG then the LP rules do not dominate during the parsing process, however, it still follows the point tracking method.

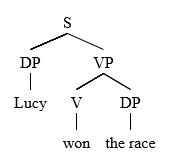
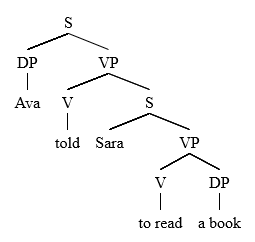
Earley Parsing in CFG

After the ID/LP Grammar has been converted to the equivalent form within a CFG, the algorithm will analyze the string. Let ${\displaystyle \mathrm {X} }$ stand for start and ${\displaystyle \alpha ,\beta ,\iota }$ stand for the elements of the string and it also represents Syntactic Categories. The algorithm then analyzes the string and identifies the following:

1. The original position of the dot; it usually begins with the left-most element of the string.
2. The current position of the dot; this predicts the following element.
3. The production of the completed string. ^[9]

(1) ${\displaystyle \mathrm {X} \longrightarrow \cdot \alpha \beta \iota }$

(2) ${\displaystyle \mathrm {X} \longrightarrow \alpha \cdot \beta \iota }$(${\displaystyle \beta }$is being predicted)

(3) ${\displaystyle \mathrm {X} \longrightarrow \alpha \beta \iota \cdot }$

The parsed strings are then used together to form a Parse List ^[10] for example:

${\displaystyle \mathrm {I} _{0}\ldots \mathrm {I} _{n}}$ ^[10]

which the list will help determine whether the completed production element (${\displaystyle \mathrm {X} \longrightarrow \alpha \beta \iota }$) is accepted within the main string. It does this by looking whether the produced individual strings are found in the Parse List. If one or all of the individual strings are not found within the Parse List, then the overall string will fail. If one or all of the individual strings are found in the Parse List, then the overall string will be accepted. ^[10]

Earley Parsing in UCFG

The UCFG is the appropriate equivalent to convert the ID/LP Grammar into in order to use the Earley Parser. ^[9] This algorithm read strings similarly to how it parses CFG, however, in this case the order of elements is not enforced; resulting in lack of LP rule enforcement. This allows some elements to be repeated within the parsed strings and the UCFG accepts empty multi-sets along with filled multi-sets within its strings. ^[9] For example:

1. The origin position of the dot; it is between the empty set and the filled set.
2. The current position of the dot which predicts the following set; the element that the dot passed will move into the empty set.
3. The production of the completed string. In this case, the position of the two sets in the origin position will swap; the filled set is on the left edge and the empty set is on the right edge. ^[9]

(1) ${\displaystyle \mathrm {X} \longrightarrow \{\}\cdot \{\alpha ,\beta ,\iota \}}$

(2) ${\displaystyle \mathrm {X} \longrightarrow \{\alpha \}\cdot \{\beta ,\iota \}}$(${\displaystyle \{\beta ,\iota \}}$are being predicted)

(3) ${\displaystyle \mathrm {X} \longrightarrow \{\alpha ,\beta ,\iota \}\cdot \{\}}$

When parsing a string that contains a number of unordered elements, the Earley Parser treats it as a Permutation, Y!, and generates each string individually instead of using one string to represent the repeated parsed strings. ^[9] Whenever the dot moves over one element, the algorithm begins to generate parsed strings of the elements on the right edge in random positions until there are no more elements in the right edge set. Let X₀ represent the original string and X₁ as the first parsed string; for example:

${\displaystyle \mathrm {X} _{0}:[\mathrm {X} \longrightarrow \{\}\cdot \{t,v,w,z\},0]}$

${\displaystyle \mathrm {X} _{1}:[\mathrm {X} \longrightarrow \{t\}\cdot \{v,w,z\},0]}$

string X₁ will produce, 3! = 6, different parsed strings of the right edge set:

(1) ${\displaystyle [\mathrm {X} \longrightarrow t.vwz,0]}$ (4) ${\displaystyle [\mathrm {X} \longrightarrow t.zvw,0]}$

(2) ${\displaystyle [\mathrm {X} \longrightarrow t.vzw,0]}$ (5) ${\displaystyle [\mathrm {X} \longrightarrow t.wvz,0]}$

(3) ${\displaystyle [\mathrm {X} \longrightarrow t.zwv,0]}$ (6) ${\displaystyle [\mathrm {X} \longrightarrow t.wzv,0]}$

The Earley Parser applies each string to the individual rules of a grammar ^[9] and this results in very large sets.The large sets is partly resulted in the conversion of ID/LP Grammar into an equivalent grammar, however, parsing the overall ID/LP Grammar is difficult to begin with. ^[9]

Shieber's Algorithm

The foundation of Shieber's Algorithm ^[9] is based on the Earley Parser for CFG, ^[10] however, it does not require the ID/LP Grammar to be converted into a different grammar ^[10] in order to be parsed. ID rules can be parsed in a separate form, S →_ID {V, NP, S}, from the LP rules, V < S. ^[10] Shieber compared parsing of a CFG to an ordered ID/LP Grammar string and Barton compared the parsing of a UCFG to an unordered ID/LP Grammar string.

Direct Parsing of an Ordered ID/LP Grammar

Parsing an ID/LP Grammar, directly, generates a set list that will determine whether the production of the string will be accepted or fail. The algorithm follows 6 Steps (the symbols used can also represents the Syntactic Categories):

1. For all of the ID rules, add ${\displaystyle [S,\mathrm {T} ,\beta ,0]}$ to the initial item in the parse list, ${\displaystyle \mathrm {I} _{0}}$. ^[10]
2. If all of the elements in ${\displaystyle \mathrm {I} _{0}}$, ${\displaystyle [\mathrm {Z} ,\lambda ,\theta ,0]}$, and the elements, ${\displaystyle [\mathrm {A} ,\alpha ,\{Z\}\cup \beta ,0]}$, of ${\displaystyle \mathrm {I} _{0}}$ does not allow Z to be preceded by ${\displaystyle \beta }$,${\displaystyle Z\nprec \beta }$, and Z is not an element of ${\displaystyle \beta }$, ${\displaystyle Z\not \in \beta }$; then the following string,${\displaystyle [\mathrm {A} ,\alpha Z,\beta ,0]}$ can be added to ${\displaystyle \mathrm {I} _{0}}$.
3. If all items, ${\displaystyle [\mathrm {A} ,\alpha ,\{Z\}\cup \beta ,0]}$, are elements of ${\displaystyle \mathrm {I} _{0}}$, then ${\displaystyle Z\nprec \beta }$, and ${\displaystyle Z\not \in \beta }$ and all of ${\displaystyle Z\longrightarrow _{\mathrm {ID} }\lambda }$ then the next item can be added to this list, ${\displaystyle [Z,T,\lambda ,0]}$.
4. This step will build the set list, ${\displaystyle \mathrm {I} _{n}}$, more. Every item, ${\displaystyle [A,\alpha ,\{q\}\cup \beta ,i]}$, that is an element of ${\displaystyle \mathrm {I} _{n-1}}$ and where ${\displaystyle q=q_{n}}$, ${\displaystyle q\nprec \beta }$ and ${\displaystyle q\not \in \beta }$ then the following item is added, ${\displaystyle [A,\alpha q,\beta ,i]}$, to ${\displaystyle \mathrm {I} _{n}}$.
5. If items, ${\displaystyle [Z,\lambda ,\theta ,i]}$, are elements of ${\displaystyle \mathrm {I} _{n}}$ and items, ${\displaystyle [A,\alpha \{Z\}\cup \beta ,k]}$, are elements of ${\displaystyle \mathrm {I} _{i}}$ where ${\displaystyle Z\nprec \beta }$, and ${\displaystyle Z\not \in \beta }$; the string, ${\displaystyle [A,\alpha Z,\beta ,k]}$, is added to ${\displaystyle \mathrm {I} _{n}}$.
6. If the items, ${\displaystyle [A,\alpha ,\{Z\}\cup \beta ,i]}$, is an element of ${\displaystyle \mathrm {I} _{n}}$ where ${\displaystyle Z\nprec \beta }$, and ${\displaystyle Z\not \in \beta }$; the string, ${\displaystyle [Z,T,\lambda ,n]}$, is added to ${\displaystyle \mathrm {I} _{n}}$.

Steps 2-3 are repeated exhaustively ^[10] until no more new items can be added and then continue on to Step 4. Steps 5-6 are also exhaustively repeated ^[10] until no further new items can be added to the set list. The string will be accepted if a string behaves or resembles the production, ${\displaystyle [S,\alpha ,\theta ,0]}$ is an element of ${\displaystyle \mathrm {I} _{n}}$. ^[10] For example:

${\displaystyle S\longrightarrow _{\mathrm {ID} }\{C,D,F\}}$

${\displaystyle C\longrightarrow _{\mathrm {ID} }\{c\}}$

${\displaystyle D\longrightarrow _{\mathrm {ID} }\{d\}}$

${\displaystyle F\longrightarrow _{\mathrm {ID} }\{f\}}$

${\displaystyle C\prec D}$

Table 1.0

Set Lists	Items
${\displaystyle \mathrm {I} _{0}}$	${\displaystyle [S,T,\{C,D,F\},0],}$ ${\displaystyle [C,T,\{c\},0],}$${\displaystyle [F,T,\{f\},0]}$
${\displaystyle \mathrm {I} _{1}}$	${\displaystyle [C,c,\emptyset ,0],}$ ${\displaystyle [S,C,\{D,F\},0],}$${\displaystyle [D,T,\{d\},1],}$${\displaystyle [F,T,\{f\},1]}$
${\displaystyle \mathrm {I} _{2}}$	${\displaystyle [F,f,\emptyset ,1],}$ ${\displaystyle [S,CF,\{D\},0],}$${\displaystyle [D,T,\{d\},2]}$
${\displaystyle \mathrm {I} _{3}}$	${\displaystyle [D,d,\emptyset ,2],}$ ${\displaystyle [S,CDF,\emptyset ,0]}$

The complete production of ${\displaystyle \mathrm {I} _{3},}$${\displaystyle [S,CDF,\emptyset ,0],}$ is accepted and produces the following production string: ${\displaystyle [_{S}[_{C}c][_{D}d][_{F}f]]}$. ^[10]

Direct Parsing of an Unordered ID/LP Grammar

The Unordered ID/LP Grammar follow the above, 6 step algorithm, in order to parse the strings. The noticeable difference is in the productions of each set list; there is one string that represents the many individual strings within one list. ^[9] The table below shows the set list of Table 1.0, ${\displaystyle [S,T,\{C,D,F\},0],}$ in an unordered grammar:

Table 2.0

Set List	Items
${\displaystyle \mathrm {I} _{0}}$	${\displaystyle [S,T,C\cdot d,f,\emptyset ,0]}$
${\displaystyle \mathrm {I} _{1}}$	${\displaystyle [S,T\cdot c,d,f,\emptyset ,0]}$
${\displaystyle \mathrm {I} _{2}}$	${\displaystyle [S,T,C,d\cdot F,\emptyset ,0]}$
${\displaystyle \mathrm {I} _{3}}$	${\displaystyle [S,T,C,D,F\cdot \emptyset ,0]}$

The complete production string, ${\displaystyle [S,T,C,D,F\cdot \emptyset ,0],}$ results in a similar string as the ordered ID/LP Grammar; however, the order of the items within the string is not enforced. The final string is accepted as it matches the original string's elements.

Notice how the Unordered version of ID/LP Grammar contains mush less strings than the UCFG; Shieber's Algorithm use one string to represent the multiple different strings for repeated elements. Both algorithms can parse Ordered Grammars equally, however, Shieber's Algorithm seems to be more efficient ^[9] when parsing an Unordered Grammar.

See also

• Generalized Phrase Structure Grammar
• Computational Linguistics
• Parsing
• Earley Parser

References

1. Gazdar, Gerald; Pullum, Geoffrey K. (1981). "Subcategorization, constituent order, and the notion 'head'". In M. Moortgat; H.v.d. Hulst; T. Hoekstra (eds.). The scope of lexical rules. pp. 107–124. ISBN   9070176521.
2. Gazdar, Gerald; Ewan H. Klein; Geoffrey K. Pullum; Ivan A. Sag (1985). Generalized Phrase Structure Grammar . Oxford: Blackwell, and Cambridge, MA: Harvard University Press. ISBN   0-674-34455-3.
3. Daniels, Mike; Meurers, Detmar (2004). "GIDLP: A grammar format for linearization-based HPSG" (PDF). Proceedings of the Eleventh International Conference on Head-Driven Phrase Structure Grammar. doi:10.21248/hpsg.2004.5. S2CID   17009554.
4. Chomsky, Noam (2007). "Biolinguistic explorations: Design, development, evolution". International Journal of Philosophical Studies. 15 (1): 1–21. doi:10.1080/09672550601143078. S2CID   144566546.
5. Chomsky, Noam (2011). "Language and other cognitive systems. What is special about language?". Language Learning and Development. 7 (4): 263–278. doi:10.1080/15475441.2011.584041. S2CID   122866773.
6. Berwick, Robert C.; et al. (2011). "Poverty of the stimulus revisited". Cognitive Science. 35 (7): 1207–1242. doi: 10.1111/j.1551-6709.2011.01189.x . PMID   21824178.
7. Bennett, Paul (1995). A Course in Generalized Phrase Structure Grammar. London: UCL Press. ISBN   1-85728-217-5.
8. Daniels, M. (2005). Generalized ID/LP grammar: a formalism for parsing linearization-based HPSG grammars. (Electronic Thesis or Dissertation). Retrieved from https://etd.ohiolink.edu/
9. Barton, Jr., G. Edward (1985). "On the Complexity of ID/LP Parsing". Computational Linguistics. 11 (4): 205–218 – via Association for Computational Linguistics.
10. Shieber, Stuart M. (1983). "Direct Parsing of ID/LP Grammars". Linguistics and Philosophy. 7 (2): 1–30 – via SRI International.