Related Research Articles

Figured bass is musical notation in which numerals and symbols appear above or below a bass note. The numerals and symbols indicate intervals, chords, and non-chord tones that a musician playing piano, harpsichord, organ, or lute should play in relation to the bass note. Figured bass is closely associated with basso continuo: a historically improvised accompaniment used in almost all genres of music in the Baroque period of Classical music, though rarely in modern music. Figured bass is also known as thoroughbass.
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale.

Atonality in its broadest sense is music that lacks a tonal center, or key. Atonality, in this sense, usually describes compositions written from about the early 20th-century to the present day, where a hierarchy of harmonies focusing on a single, central triad is not used, and the notes of the chromatic scale function independently of one another. More narrowly, the term atonality describes music that does not conform to the system of tonal hierarchies that characterized European classical music between the seventeenth and nineteenth centuries. "The repertory of atonal music is characterized by the occurrence of pitches in novel combinations, as well as by the occurrence of familiar pitch combinations in unfamiliar environments".

Music theory is the study of the practices and possibilities of music. The Oxford Companion to Music describes three interrelated uses of the term "music theory": The first is the "rudiments", that are needed to understand music notation ; the second is learning scholars' views on music from antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built."
In music theory, a tetrachord is a series of four notes separated by three intervals. In traditional music theory, a tetrachord always spanned the interval of a perfect fourth, a 4:3 frequency proportion —but in modern use it means any four-note segment of a scale or tone row, not necessarily related to a particular tuning system.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions. The minor third is one of two commonly occurring thirds. It is called minor because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones. The minor third is a skip melodically.
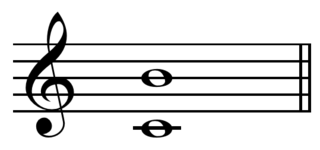
In music from Western culture, a seventh is a musical interval encompassing seven staff positions, and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two. The major seventh spans eleven semitones, its smaller counterpart being the minor seventh, spanning ten semitones. For example, the interval from C to B is a major seventh, as the note B lies eleven semitones above C, and there are seven staff positions from C to B. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones.
The intervals from the tonic (keynote) in an upward direction to the second, to the third, to the sixth, and to the seventh scale degrees (of a major scale are called major.

Density 21.5 is a composition for solo flute written by Edgard Varèse in 1936 and revised in 1946. The piece was composed at the request of Georges Barrère for the premiere of his platinum flute, the density of platinum being close to 21.5 grams per cubic centimetre.
In music, unified field is the 'unity of musical space' created by the free use of melodic material as harmonic material and vice versa.
Voice leading is the linear progression of individual melodic lines and their interaction with one another to create harmonies, typically in accordance with the principles of common-practice harmony and counterpoint.

The chromatic circle is a clock diagram for displaying relationships among the 12 equal-tempered pitch classes making up the familiar chromatic scale on a circle.
"Cognitive Constraints on Compositional Systems" is an essay by Fred Lerdahl that cites Pierre Boulez's Le Marteau sans maître (1955) as an example of "a huge gap between compositional system and cognized result," though he "could have illustrated just as well with works by Milton Babbitt, Elliott Carter, Luigi Nono, Karlheinz Stockhausen, or Iannis Xenakis". To explain this gap, and in hopes of bridging it, Lerdahl proposes the concept of a musical grammar, "a limited set of rules that can generate indefinitely large sets of musical events and/or their structural descriptions". He divides this further into compositional grammar and listening grammar, the latter being one "more or less unconsciously employed by auditors, that generates mental representations of the music". He divides the former into natural and artificial compositional grammars. While the two have historically been fruitfully mixed, a natural grammar arises spontaneously in a culture while an artificial one is a conscious invention of an individual or group in a culture; the gap can arise only between listening grammar and artificial grammars. To begin to understand the listening grammar, Lerdahl and Ray Jackendoff created a theory of musical cognition, A Generative Theory of Tonal Music. That theory is outlined in the essay.
In music cognition and musical analysis, the study of melodic expectation considers the engagement of the brain's predictive mechanisms in response to music. For example, if the ascending musical partial octave "do-re-mi-fa-sol-la-ti-..." is heard, listeners familiar with Western music will have a strong expectation to hear or provide one more note, "do", to complete the octave.

In music, a step, or conjunct motion, is the difference in pitch between two consecutive notes of a musical scale. In other words, it is the interval between two consecutive scale degrees. Any larger interval is called a skip, or disjunct motion.

Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.
A generative theory of tonal music (GTTM) is a theory of music conceived by American composer and music theorist Fred Lerdahl and American linguist Ray Jackendoff and presented in the 1983 book of the same title. It constitutes a "formal description of the musical intuitions of a listener who is experienced in a musical idiom" with the aim of illuminating the unique human capacity for musical understanding.
In music cognition, melodic fission, is a phenomenon in which one line of pitches is heard as two or more separate melodic lines. This occurs when a phrase contains groups of pitches at two or more distinct registers or with two or more distinct timbres.
Musicology commonly classifies scales as either hemitonic or anhemitonic. Hemitonic scales contain one or more semitones, while anhemitonic scales do not contain semitones. For example, in traditional Japanese music, the anhemitonic yo scale is contrasted with the hemitonic in scale. The simplest and most commonly used scale in the world is the atritonic anhemitonic "major" pentatonic scale. The whole tone scale is also anhemitonic.
The Tone Clock, and its related compositional theory Tone-Clock Theory, is a post-tonal music composition technique, developed by composers Peter Schat and Jenny McLeod. Music written using tone-clock theory features a high economy of musical intervals within a generally chromatic musical language. This is because tone-clock theory encourages the composer to generate all their harmonic and melodic material from a limited number of intervallic configurations. Tone-clock theory is also concerned with the way that the three-note pitch-class sets can be shown to underlie larger sets, and considers these triads as a fundamental unit in the harmonic world of any piece. Because there are twelve possible triadic prime forms, Schat called them the 'hours', and imagined them arrayed in a clock face, with the smallest hour in the 1 o'clock position, and the largest hour in the 12 o'clock position. A notable feature of Tone-Clock Theory is 'tone-clock steering': transposing and/or inverting hours so that each note of the chromatic aggregate is generated once and once only.
References
- Cross, I. (1995) "Review of The analysis and cognition of melodic complexity: the implication-realization model, by E. Narmour, Univ. of Chicago Press, Chicago, 1992." Music Perception12(4), 486–509.
- Meyer, L. B. (1956). Emotion and Meaning in Music. Chicago: University of Chicago Press. ISBN 0-226-52139-7.
- Meyer, L. B. (1973) Explaining Music: Essays and explorations. Chicago: University of Chicago Press. ISBN 0-226-52142-7.
- Narmour, E. (1977) Beyond Schenkerism: The Need for Alternatives in Music Analysis. Chicago: University of Chicago Press. ISBN 0-226-56847-4.
- Narmour, E. (1989) "The 'Genetic code' of melody: Cognitive structures generated by the implication-realization model. In Music and the cognitive sciences, ed. Stephen McAdams and Irène Deliège. London: Harwood Academic.
- Narmour, E. (1990) The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago: University of Chicago Press. ISBN 0-226-56845-8.
- Narmour, E. (1992) The Analysis and Cognition of Melodic Complexity: The Implication-Realization Model. Chicago: University of Chicago Press. ISBN 0-226-56842-3.
- Schellenberg, E. (1997). "Simplifying the Implication-Realization Model of Musical Expectancy." Music Perception14(3), 295–318.