In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as

In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero.
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. It can be used to calculate the informational difference between measurements.
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of exact simulation method. The method works for any distribution in with a density.
In estimation theory and statistics, the Cramér–Rao bound (CRB), Cramér–Rao lower bound (CRLB), Cramér–Rao inequality, Frechét–Darmois–Cramér–Rao inequality, or information inequality expresses a lower bound on the variance of unbiased estimators of a deterministic parameter. This term is named in honor of Harald Cramér, Calyampudi Radhakrishna Rao, Maurice Fréchet and Georges Darmois all of whom independently derived this limit to statistical precision in the 1940s.
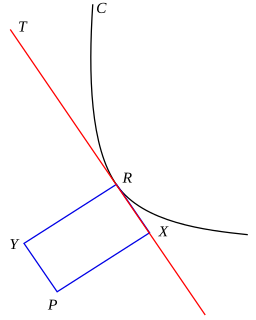
The pedal curve results from the orthogonal projection of a fixed point on the tangent lines of a given curve. More precisely, for a plane curve C and a given fixed pedal pointP, the pedal curve of C is the locus of points X so that the line PX is perpendicular to a tangent T to the curve passing through the point X. Conversely, at any point R on the curve C, let T be the tangent line at that point R; then there is a unique point X on the tangent T which forms with the pedal point P a line perpendicular to the tangent T – the pedal curve is the set of such points X, called the foot of the perpendicular to the tangent T from the fixed point P, as the variable point R ranges over the curve C.
In soil science, pedotransfer functions (PTF) are predictive functions of certain soil properties using data from soil surveys.

In geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.

Infiltration is the process by which water on the ground surface enters the soil. It is commonly used in both hydrology and soil sciences. The infiltration capacity is defined as the maximum rate of infiltration. It is most often measured in meters per day but can also be measured in other units of distance over time if necessary. The infiltration capacity decreases as the soil moisture content of soils surface layers increases. If the precipitation rate exceeds the infiltration rate, runoff will usually occur unless there is some physical barrier.

In analytical mechanics, a branch of theoretical physics, Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
In physics and engineering, the radiative heat transfer from one surface to another is the equal to the difference of incoming and outgoing radiation from the first surface. In general, the heat transfer between surfaces is governed by temperature, surface emissivity properties and the geometry of the surfaces. The relation for heat transfer can be written as an integral equation with boundary conditions based upon surface conditions. Kernel functions can be useful in approximating and solving this integral equation.

The finite water-content vadose zone flux method represents a one-dimensional alternative to the numerical solution of Richards' equation for simulating the movement of water in unsaturated soils. The finite water-content method is an ordinary differential equation alternative to the Richards partial differential equation. The Richards equation is difficult to approximate in general because it does not have a closed-form analytical solution except in a few cases. The finite water-content method, is perhaps the first generic replacement for the numerical solution of the Richards' equation. The finite water-content solution has several advantages over the Richards equation solution. First, as an ordinary differential equation it is explicit, guaranteed to converge and computationally inexpensive to solve. Second, using a finite volume solution methodology it is guaranteed to conserve mass. The finite water content method readily simulates sharp wetting fronts, something that the Richards solution struggles with. The main limiting assumption required to use the finite water-content method is that the soil be homogeneous in layers.
The soil moisture velocity equation is useful for calculation of the speed that water moves vertically through a soil, a process known as infiltration. The equation is equivalent to Richards' equation with a key difference. The dependent variable is the position of the wetting front , which is a function of the water content and media properties. The soil moisture velocity equation consists of two terms. The first "advection-like" term, was developed by Talbot and Ogden and extended to the water table by Ogden et al. as verified against data collected in a column experimental that was patterned after the famous experiment by Childs & Poulovassilis (1962) and against exact solutions.