Related Research Articles

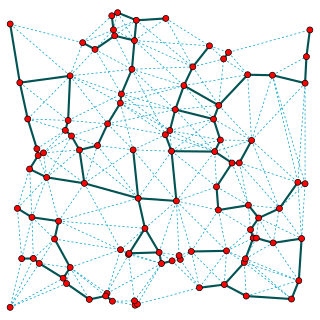
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
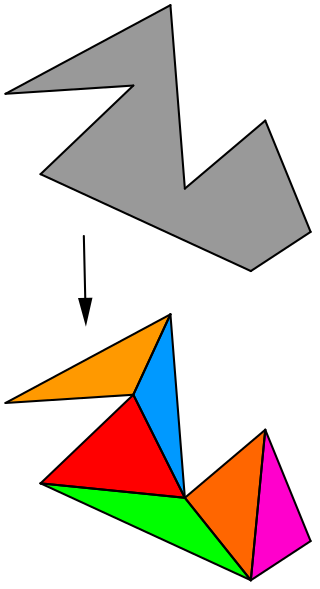
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.
JTS Topology Suite is an open-source Java software library that provides an object model for Euclidean planar linear geometry together with a set of fundamental geometric functions. JTS is primarily intended to be used as a core component of vector-based geomatics software such as geographical information systems. It can also be used as a general-purpose library providing algorithms in computational geometry.

In mathematics and computational geometry, the Gabriel graph of a set of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph with vertex set in which any two distinct points and are adjacent precisely when the closed disc having as a diameter contains no other points. Another way of expressing the same adjacency criterion is that and should be the two closest given points to their midpoint, with no other given point being as close. Gabriel graphs naturally generalize to higher dimensions, with the empty disks replaced by empty closed balls. Gabriel graphs are named after K. Ruben Gabriel, who introduced them in a paper with Robert R. Sokal in 1969.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.
Parallel mesh generation in numerical analysis is a new research area between the boundaries of two scientific computing disciplines: computational geometry and parallel computing. Parallel mesh generation methods decompose the original mesh generation problem into smaller subproblems which are solved (meshed) in parallel using multiple processors or threads. The existing parallel mesh generation methods can be classified in terms of two basic attributes:
- the sequential technique used for meshing the individual subproblems and
- the degree of coupling between the subproblems.

In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points and by an edge whenever there does not exist a third point that is closer to both and than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.
In mesh generation, Delaunay refinements are algorithms for mesh generation based on the principle of adding Steiner points to the geometry of an input to be meshed, in a way that causes the Delaunay triangulation or constrained Delaunay triangulation of the augmented input to meet the quality requirements of the meshing application. Delaunay refinement methods include methods by Chew and by Ruppert.

Herbert Edelsbrunner is a computer scientist working in the field of computational geometry, the Arts & Science Professor of Computer Science and Mathematics at Duke University, Professor at the Institute of Science and Technology Austria (ISTA), and the co-founder of Geomagic, Inc. He was the first of only three computer scientists to win the National Science Foundation's Alan T. Waterman Award.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation as edges, unlike the Delaunay triangulation itself which is based purely on the position of a given set of vertices without regard to how they should be connected by edges. It can be computed efficiently and has applications in geographic information systems and in mesh generation.
In computational geometry, an alpha shape, or α-shape, is a family of piecewise linear simple curves in the Euclidean plane associated with the shape of a finite set of points. They were first defined by Edelsbrunner, Kirkpatrick & Seidel (1983). The alpha-shape associated with a set of points is a generalization of the concept of the convex hull, i.e. every convex hull is an alpha-shape but not every alpha shape is a convex hull.
Algorithmic Geometry is a textbook on computational geometry. It was originally written in the French language by Jean-Daniel Boissonnat and Mariette Yvinec, and published as Géometrie algorithmique by Edusciences in 1995. It was translated into English by Hervé Brönnimann, with improvements to some proofs and additional exercises, and published by the Cambridge University Press in 1998.
Reverse-search algorithms are a class of algorithms for generating all objects of a given size, from certain classes of combinatorial objects. In many cases, these methods allow the objects to be generated in polynomial time per object, using only enough memory to store a constant number of objects. They work by organizing the objects to be generated into a spanning tree of their state space, and then performing a depth-first search of this tree.
References
- Green, P. J.; Sibson, R. (1978), "Computing Dirichlet tessellations in the plane", The Computer Journal, 21 (2): 168–173, doi:10.1093/comjnl/21.2.168, MR 0485467 .
- Lawson, C. (1977), "Software for C1 surface interpolation", in Rice, J. R. (ed.), Mathematical Software III, NY: Academic Press, pp. 161–194.
- Devroye, Luc; Lemaire, Christophe; Moreau, Jean-Michel (2004), "Expected time analysis for Delaunay point location", Computational Geometry: Theory and Applications , 29 (2): 61–89, doi: 10.1016/j.comgeo.2004.02.002 , MR 2082208 .
- Devroye, L.; Mücke, E. P.; Zhu, Binhai (1998), "A note on point location in Delaunay triangulations of random points", Algorithmica , 22 (4): 477–482, CiteSeerX 10.1.1.15.8612 , doi:10.1007/PL00009234, MR 1701623, S2CID 3000041 .
- Mücke, Ernst P.; Saias, Isaac; Zhu, Binhai (1999), "Fast randomized point location without preprocessing in two- and three-dimensional Delaunay triangulations", Special issue for 12th ACM Symposium on Computational Geometry (Philadelphia, PA, 1996), Computational Geometry: Theory and Applications , 12 (1–2): 63–83, doi: 10.1016/S0925-7721(98)00035-2 , MR 1677599 .