
In mathematics convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, it differs from cross-correlation only in that either f (x) or g(x) is reflected about the y-axis; thus it is a cross-correlation of f (x) and g(−x), or f (−x) and g(x). For continuous functions, the cross-correlation operator is the adjoint of the convolution operator.
In mathematics, a metric space is a set together with a metric on the set. The metric is a function that defines a concept of distance between any two members of the set, which are usually called points. The metric satisfies a few simple properties. Informally:
In mathematics, the Cauchy–Schwarz inequality, also known as the Cauchy–Bunyakovsky–Schwarz inequality, is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, vector algebra and other areas. It is considered to be one of the most important inequalities in all of mathematics.
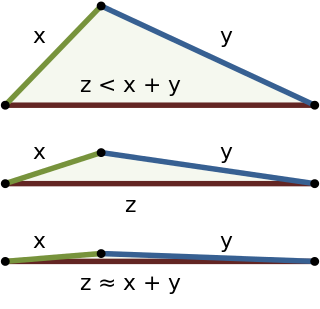
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that
In mathematics, especially functional analysis, Bessel's inequality is a statement about the coefficients of an element in a Hilbert space with respect to an orthonormal sequence.

In mathematics, the Riemann–Lebesgue lemma, named after Bernhard Riemann and Henri Lebesgue, is of importance in harmonic analysis and asymptotic analysis.
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.
In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and other martingales. Quadratic variation is just one kind of variation of a process.
In mathematics, a constraint is a condition of an optimization problem that the solution must satisfy. There are several types of constraints—primarily equality constraints, inequality constraints, and integer constraints. The set of candidate solutions that satisfy all constraints is called the feasible set.
A second-order cone program (SOCP) is a convex optimization problem of the form
In mathematical analysis, the Schur test, named after German mathematician Issai Schur, is a bound on the operator norm of an integral operator in terms of its Schwartz kernel.
In mathematics, in the field of functional analysis, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar and Elias Stein. It may be used to obtain information on the operator norm on an operator, acting from one Hilbert space into another when the operator can be decomposed into almost orthogonal pieces. The original version of this lemma (for self-adjoint and mutually commuting operators) was proved by Mischa Cotlar in 1955 and allowed him to conclude that the Hilbert transform is a continuous linear operator in without using the Fourier transform. A more general version was proved by Elias Stein.
Subgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function. When the objective function is differentiable, sub-gradient methods for unconstrained problems use the same search direction as the method of steepest descent.
In mathematics, the Hardy–Littlewood maximal operatorM is a significant non-linear operator used in real analysis and harmonic analysis. It takes a locally integrable function f : Rd → C and returns another function Mf that, at each point x ∈ Rd, gives the maximum average value that f can have on balls centered at that point. More precisely,
In mathematics, the Marcinkiewicz–Zygmund inequality, named after Józef Marcinkiewicz and Antoni Zygmund, gives relations between moments of a collection of independent random variables. It is a generalization of the rule for the sum of variances of independent random variables to moments of arbitrary order. It is a special case of the Burkholder-Davis-Gundy inequality in the case of discrete-time martingales.

Rodion Osievich Kuzmin was a Russian mathematician, known for his works in number theory and analysis. His name is sometimes transliterated as Kusmin. He was an Invited Speaker of the ICM in 1928 in Bologna.
In mathematics, Young's convolution inequality is a mathematical inequality about the convolution of two functions, named after William Henry Young.
Kallman is a surname of the following people:

Gian-Carlo Rota was an Italian-born American mathematician and philosopher.
Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.







