Kantorovich inequality

Last updated April 13, 2019

In mathematics, the Kantorovich inequality is a particular case of the Cauchy–Schwarz inequality, which is itself a generalization of the triangle inequality.

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

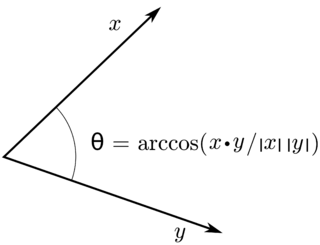
In mathematics, the Cauchy–Schwarz inequality, also known as the Cauchy–Bunyakovsky–Schwarz inequality, is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, vector algebra and other areas. It is considered to be one of the most important inequalities in all of mathematics.

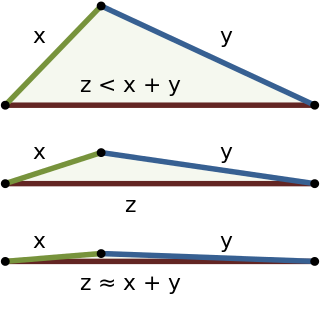
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If $x$ , $y$ , and $z$ are the lengths of the sides of the triangle, with no side being greater than $z$ , then the triangle inequality states that

The triangle inequality states that the length of two sides of any triangle, added together, will be equal to or greater than the length of the third side. In simplest terms, the Kantorovich inequality translates the basic idea of the triangle inequality into the terms and notational conventions of linear programming. (See vector space, inner product, and normed vector space for other examples of how the basic ideas inherent in the triangle inequality—line segment and distance—can be generalized into a broader context.)

Linear programming is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.

A vector space is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms, listed below.

In mathematics, a normed vector space is a vector space over the real or complex numbers, on which a norm is defined. A norm is the formalization and the generalization to real vector spaces of the intuitive notion of distance in the real world. A norm is a real-valued function defined on the vector space that has the following properties:

The zero vector, 0, has zero length; every other vector has a positive length.
Multiplying a vector by a positive number changes its length without changing its direction. Moreover,
The triangle inequality holds. That is, taking norms as distances, the distance from point A through B to C is never shorter than going directly from A to C, or the shortest distance between any two points is a straight line.

More formally, the Kantorovich inequality can be expressed this way:

Let

p_{i}\geq 0,\quad 0<a\leq x_{i}\leq b{\text{ for }}i=1,\dots ,n.

Let

A_{n}=\{1,2,\dots ,n\}.

Then

{\begin{aligned}&{}\qquad \left(\sum _{i=1}^{n}p_{i}x_{i}\right)\left(\sum _{i=1}^{n}{\frac {p_{i}}{x_{i}}}\right)\\&\leq {\frac {(a+b)^{2}}{4ab}}\left(\sum _{i=1}^{n}p_{i}\right)^{2}-{\frac {(a-b)^{2}}{4ab}}\cdot \min \left\{\left(\sum _{i\in X}p_{i}-\sum _{j\in Y}p_{j}\right)^{2}\,:\,{X\cup Y=A_{n}},{X\cap Y=\varnothing }\right\}.\end{aligned}}

The Kantorovich inequality is used in convergence analysis; it bounds the convergence rate of Cauchy's steepest descent.

Equivalents of the Kantorovich inequality have arisen in a number of different fields. For instance, the Cauchy–Schwarz–Bunyakovsky inequality and the Wielandt inequality are equivalent to the Kantorovich inequality and all of these are, in turn, special cases of the Hölder inequality.

The Kantorovich inequality is named after Soviet economist, mathematician, and Nobel Prize winner Leonid Kantorovich, a pioneer in the field of linear programming.

The Nobel Prize is a set of annual international awards bestowed in several categories by Swedish and Norwegian institutions in recognition of academic, cultural, or scientific advances.

Leonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources. He is regarded as the founder of linear programming. He was the winner of the Stalin Prize in 1949 and the Nobel Memorial Prize in Economic Sciences in 1975.

There is also Matrix version of the Kantrovich inequality due to Marshall and Olkin.

Related Research Articles

In probability theory, the expected value of a random variable, intuitively, is the long-run average value of repetitions of the same experiment it represents. For example, the expected value in rolling a six-sided die is 3.5, because the average of all the numbers that come up is 3.5 as the number of rolls approaches infinity. In other words, the law of large numbers states that the arithmetic mean of the values almost surely converges to the expected value as the number of repetitions approaches infinity. The expected value is also known as the expectation, mathematical expectation, EV, average, mean value, mean, or first moment.

Inner product space vector space with an additional structure called an inner product

In linear algebra, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.

In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series $is said to converge absolutely if for some real number . Similarly, an improper integral of a function,, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if$

In probability theory, Chebyshev's inequality guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/k² of the distribution's values can be more than k standard deviations away from the mean. The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers.

In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of $L p$ spaces.

In mathematical analysis, the Minkowski inequality establishes that the L^p spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of L^p(S). Then f + g is in L^p(S), and we have the triangle inequality

In calculus, the squeeze theorem, also known as the pinching theorem, the sandwich theorem, the sandwich rule, and sometimes the squeeze lemma, is a theorem regarding the limit of a function.

In probability theory, the Chernoff bound, named after Herman Chernoff but due to Herman Rubin, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is a sharper bound than the known first- or second-moment-based tail bounds such as Markov's inequality or Chebyshev's inequality, which only yield power-law bounds on tail decay. However, the Chernoff bound requires that the variates be independent – a condition that neither Markov's inequality nor Chebyshev's inequality require, although Chebyshev's inequality does require the variates to be pairwise independent.

In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin Louis Cauchy.

In linear algebra, functional analysis, and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to each vector in a vector space—except for the zero vector, which is assigned a length of zero. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.

In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.

In mathematics, the Riesz–Fischer theorem in real analysis is any of a number of closely related results concerning the properties of the space L² of square integrable functions. The theorem was proven independently in 1907 by Frigyes Riesz and Ernst Sigismund Fischer.

In probability theory and statistics, the Rademacher distribution is a discrete probability distribution where a random variate X has a 50% chance of being +1 and a 50% chance of being -1.

In mathematics, majorization is a preorder on vectors of real numbers. For a vector $, we denote by the vector with the same components, but sorted in descending order. Given, we say that weakly majorizes from below written as iff$

The Kantorovich theorem is a mathematical statement on the convergence of Newton's method. It was first stated by Leonid Kantorovich in 1940.

In functional analysis, the dual norm is a measure of the "size" of each continuous linear functional defined on a normed vector space.

In mathematics, the second moment method is a technique used in probability theory and analysis to show that a random variable has positive probability of being positive. More generally, the "moment method" consists of bounding the probability that a random variable fluctuates far from its mean, by using its moments.

In mathematics, Welch bounds are a family of inequalities pertinent to the problem of evenly spreading a set of unit vectors in a vector space. The bounds are important tools in the design and analysis of certain methods in telecommunication engineering, particularly in coding theory. The bounds were originally published in a 1974 paper by L. R. Welch.

References

Weisstein, Eric W. "Kantorovich Inequality". MathWorld .
Cauchy-Schwarz inequality at PlanetMath.org .
Mathematical Programming Glossary entry on "Kantorovich inequality"
MARSHALL A. W. and OLKIN, I., Matrix versions of the Cauchy and Kantorovieh inequatities. Aequationes Mathematicae 40 (1990), pp. 89–93.

Eric Wolfgang Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science (ScienceWorld). He is the author of the CRC Concise Encyclopedia of Mathematics. He currently works for Wolfram Research, Inc.

MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign.

PlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org, Ltd".

External links

Biography of Leonid Vitalyevich Kantorovich

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.